Filtr Kalmana

Wstęp.

O filtrze Kalmana słyszał zapewne każdy, kto miał do czynienia z elektroniką lub naukami pokrewnymi. Od czasu jego wynalezienia minęło już ponad 50 lat (algorytm ochrzczono imieniem jego autora: Rudolfa Emila Kalmana) i zdążył się już zadomowić na dobre wszędzie tam, gdzie zachodzi potrzeba sterowania obiektami w warunkach niepewności. Każdy automatyk powinien zatem przyswoić sobie chociaż minimum wiedzy potrzebnej do wykorzystania FK w praktycznych zastosowaniach. Moje pierwsze spotkanie z filtrem miało miejsce jeszcze na studiach jednak nie było wystarczająco dużo czasu w ramach laboratorium żeby na spokojnie przemyśleć całość zagadnienia dlatego postanowiłem zsyntezować dostępne mi materiały i stworzyć zwięzły ale kompletny opis FK, wraz z przykładami, które w miarę jasno wyjaśniają gdzie i jak warto użyć FK.

Wstęp 2.

Zanim przejdę do konkretów chciałem zwrócić uwagę jeszcze na kilka spraw. W niniejszym opracowaniu znajdą się skrypty implementujące omawiane przykłady gotowe do uruchomienia w Matlabie/Octave. Polecam szczególnie to drugie środowisko ponieważ jest darmowe, a od niedawna dostępne jest domyślnie z GUI co znacząca ułatwia pracę i upodabnia to narzędzie do swojego pierwowzoru. W przykładach użyto dwóch dodatkowych funkcji:

Plik: square.m

function [y] = square (t, freq, duty)
    tt = numel(t);
    y = zeros(1,tt);
    div = 1 / freq; % okres
    z = div * duty / 100; % dlugosc stanu wysokiego
    
    for i = 1:tt
        r = rem(t(i), div);
        if (r < z)
            y(i) = 1;
        end
    end
end

Funkcja square generuje przebieg prostokątny dla zadanego wektora czasu t, częstotliwości freq i wypełnieniu duty (w %). Implementację jednej iteracji FK realizuje funkcja:

Plik: KalmanFilter.m

function [newX,newP] = KalmanFilter (A,B,H,q,W,R,u,y,xPost,pPost,dt)
    Q = q * W * q';
    I = eye(size(A,1));
    % predykcja
    xPrio = A * xPost + B * u;
    pPrio = A * pPost * A' + Q;
    % filtracja
    K = pPrio * H' * (H * pPrio * H' + R)^-1;
    newX = xPrio + K * (y - H * xPrio);
    newP = (I - K * H) * pPrio;
end

której parametrami są kolejne macierze niezbędne do realizacji FK, wektor wejść, wyjść, poprzednia wartość estymaty stanu, poprzednia wartość macierzy kowariancji błędu filtracji oraz okres próbkowania.

Informacje ogólne.

Filtr Kalmana jest optymalnym estymatorem stanu układu dynamicznego. Należy tutaj jednak przywołać kilka założeń, które są niezbędne (choć czasem przemilczane), aby filtr działał jak należy. Są to:

• dany jest układ dynamiczny w postaci układu równań różnicowych liniowych (dla tradycyjnego filtru) lub równań różnicowych nieliniowych (rozszerzony filtr Kalmana),
• wejścia i wyjścia układu są dostępne pomiarowo,
• zakłócenia oddziałujące na stan układu oraz szumy pomiarowe mają rozkład normalny o wartości oczekiwanej równej 0 i znanych wariancjach.
• wektory $w$, $v$ oraz $x$ (opisane poniżej) są wzajemnie niezależne.

Jak nietrudno się domyślić, filtr Kalmana używany jest przede wszystkim do odszumiania pomiarów oraz odtwarzania zmiennych stanu, które nie są dostępne pomiarowo w sposób bezpośredni.

Równania modelu.

Dany jest model dyskretnego układu dynamicznego w postaci: $$\begin{cases} x_{k+1}=Ax_k+Bu_k+w_k \\ y_k=Hx_k+v_k, \end{cases}$$ gdzie: $x$ - stan układu, $u$ - wejście, $y$ - wyjście, zaś $k$ oznacza dyskretną chwilę czasu $k$. Sam układ opisany jest macierzami: $A$ - macierz przejścia, $B$ - macierz wejścia, $H$ - macierz wyjścia. Wektor $w$ jest wektorem szumu procesowego o zerowej wartości oczekiwanej i znanej macierzy kowariancji $Q$: $w_k\sim N\left(0,Q_k\right)$. Wektor $v$ to wektor szumu pomiarowego o podobnych założeniach co $w$ oraz znanej macierzy kowariancji $R$: $v_k\sim N\left(0,R_k\right)$. Aby możliwe było stworzenie poprawnego FK konieczne jest sprowadzenie modelu procesu do powyższej postaci oraz wyznaczenie obydwu macierzy szumów.

Równania filtru Kalmana.

Równania FK można podzielić na dwie części:

• część predykcyjną - dokonuje predykcji stanu w chwili $k$ na podstawie estymaty stanu i sterowania z chwili poprzedniej: $$ \hat{x}_{k|k-1}=A\hat{x}_{k-1|k-1}+Bu_{k-1}\\ P_{k|k-1}=AP_{k-1|k-1}A^T+Q, $$ gdzie: $\hat{x}_{k|k-1}$ - ocena stanu a priori (przed pomiarem), $\hat{x}_{k|k}$ - wstymata stanu a posteriori (po pomiarze), $P_{k|k-1}$ - macierz kowariancji błędu predykcji, $P_{k|k}$ - macierz kowariancji błędu filtracji, $Q$ - macierz kowariancji szumu procesowego.
• część filtracyjną - dokonuje aktualizacji estymatu stanu i macierzy błędu kowariancji stanu na podstawie pomiaru wejść w chwili obecnej: $$ K=P_{k|k-1}H^T\left(HP_{k|k-1}H^T+R\right)^{-1}\\ \hat{x}_{k|k}=\hat{x}_{k|k-1}+K\left(y_k-H\hat{x}_{k|k-1}\right)\\ P_{k|k}=\left(I-KH\right)P_{k|k-1}, $$ gdzie: $K$ - wzmocnienie filtru Kalmana, $R$ - macierz kowariancji szumu pomiarowego. Wzmocnienie filtru, zależne od $R$ jest informacją o tym, w jaki sposób informacja pochodząca z pomiarów wpływać ma na korekcję estymatu stanu. Dla dużej wartości $K$ (małego zakłócenia stanu w $R$) pomiary będą miały istotny wpływ na wartość $\hat{x}_{k|k}$. Macierz $I$ to macierz jednostkowa o odpowiednim rozmiarze.

Uwagi implementacyjne.

Przed przystąpieniem do implementacji FK chciałbym zwrócić uwagę jeszcze na kilka kwestii.

• Inicjalizacja algorytmu - do rozpoczęcia działania filtra konieczne jest ustalenie dwóch wielkości: $\hat{x}_{0|0}$ oraz $P_{0|0}$, które wykorzystywane są w pierwszej fazie predykcji algorytmu. Wektor $\hat{x}_{0|0}$ jest wartością oczekiwaną stanu w chwili 0, zaś macierz $P_{0|0}$ można przyjąć za równą wartości macierzy kowariancji szumu procesowego. Obie te wielkości można również ustalić arbitralnie, przy czym jeśli nie znamy początkowego stanu układu macierz $P_{0|0}$ powinna być odpowiednio "duża".
• Wymiarowość macierzy - wprawdzając wymiary macierzy: $A_{m\times m}$, $x_{m \times 1}$, $B_{m \times n}$, $u_{n \times 1}$, $w_{m \times 1}$ oraz $y_{o \times 1}$, $H_{o \times m}$ i $v_{o \times 1}$ oraz korzystając z dostępnych równań można wyznaczyć następujące rozmiary macierzy: $P_{m \times m}$, $K_{m \times o}$, $Q_{m \times m}$ i $R_{o \times o}$.
• Macierz kowariancji szumu pomiarowego $R$ - zakładając, że szumy pomiarowe są niezależne (nieskorelowane), macierz $R$ przymuje postać diagonalną z wariancjami zakłóceń na głównej przekątnej: $$ R=E\left[vv^T\right]=\begin{bmatrix} \sigma_{1}^2 & 0 & \ldots & 0\\ 0 & \sigma_{2}^2 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \ldots & \sigma_{o}^2 \end{bmatrix}. $$ Wariancje wchodzące w skład macierzy $R$ są zazwyczaj łatwe do określenia dzięki znajomości parametrów urządzeń pomiarowych.
• Macierz kowariancji szumu procesowego $Q$ - dana jest ona w postaci: $$ Q=qWq^T, $$ gdzie: $q$ - macierz modelująca zakłócenia stanu. Macierz $q$ zazwyczaj wyznaczana jest poprzez wstawienie w model procesu zależności określająch obecność zakłóceń oddziałujących na stan tj.: $$ x^i_k=\tilde{x}^i_k+w^i_k, $$ gdzie indeks górny oznacza i-ty element wektora stanu zaś dolny - k-ty krok działania FK. Macierz kowariancji $W$ zakłóceń stanu określona jest jako: $$ W=E\left[ww^T\right], $$ gdzie: $w$ - wektor zakłóceń zawierający wariancje zakłóceń poszczególnych składowych stanu (analogicznie do macierzy $R$). W praktyce można potraktować macierz $W$ jako parametr strojący filtr oraz przyjąć, że składowe zakłócenia stanu są niezależne co upraszcza macierz $W$ do postaci: $$ W=I\alpha, $$ gdzie: $\alpha$ - parametr strojenia. Im jest on mniejszy tym wolniejsza odpowiedź filtru objawiająca się bardziej gładkim filtrowaniem ale gorszymi własnościami nadążnymi.
• W praktyce spotkać się można z nieco mniej skomplikowanym podejściem do strojenia FK. Macierze $Q$ i $R$ ustalane są arbitralnie jako macierze diagonalne z dobranymi doświadczalnie wartościami na głównych przekątnych.
• Macierze $K$, $P_{k|k-1}$ oraz $P_{k|k}$ można wyznaczyć off-line, czyli niezależnie od działania filtru.

Przykład 1. Przypadek skalarny.

Najprostszym przykładem wykorzystania FK jest estymacja stanu obiektu, którego model sprowadzić można do postaci: $$ x_{k+1}=x_k\\ $$ stąd: $A=1$, $B=0$ i $H=1$. Stan jest wielkością skalarną stąd wektory $w_k$ i $v_k$ również przyjmują postać skalarną. Macierz kowariancji szumu pomiarowego $R$ sprowadza się bezpośrednio do wariancji tego szumu: $$ R=E\left[vv^T\right]=\sigma_{v}^2. $$ Do wyznaczenia macierzy $Q$ należy wprowadzić zależność opisującą wpływ zakłóceń stanu w chwili i-tej: $$ x_k=\tilde{x}_k+w_k. $$ Podstawiając tę formułę do równania modelu oraz uwzględniając fakt, że wyjściem jest bezpośrednio mierzony stan dodatkowo obarczony szumem pomiarowym otrzymujemy: $$ x_{k+1}=x_k+w_k\\ y_k=x_k+v_k. $$ Przyrównując to do ogólnego równania filtru otrzymujemy $q=1$, stąd macierz kowariancji szumu procesowego dana jest: $$ Q=W=E\left[ww^T\right]=\sigma_{w}^2. $$ Równania filtru Kalmana dla takiego modelu upraszczają się do bardzo kompaktowej formy: $$ \hat{x}_{k|k-1}=\hat{x}_{k|k}\\ P_{k|k-1}=P_{k|k}+Q\\ K=P_{k|k-1}\left(P_{k|k-1}+R\right)^{-1}\\ \hat{x}_{k|k}=\hat{x}_{k|k-1}+K\left(y_k-\hat{x}_{k|k-1}\right)\\ P_{k|k}=\left(1-K\right)P_{k|k-1}. $$

Taka postać FK może posłużyć do odszumiania praktycznie dowolnych danych. Strojenie takiego filtru opiera się tylko na doborze wartości parametrów Q i R. Ten prosty model ma niewątpliwą zaletę w postaci łatwości implementacji i niewielkiego narzutu obliczeniowego, szczególnie istotnego chociażby w systemach mikroprocesorowych. Skrypt realizujący powyższe działania wraz z przykładowym wywołaniem przedstawiono poniżej:

Plik: kalman1.m

tSim = 20;
h = 0.1;
t = 0:h:tSim;
tt = numel(t);

% odchylenie standardowe zaklocenia
sigma_y = 1;

% 1.5 okresu sygnalu prostokatego
y = square(t,1/tSim * 1.5,50) * 10;
y = y + randn(1,tt) * sigma_y;

% macierze kowariancji
Q = 0.1;
R = sigma_y^2;

% FK
xHat = zeros(1,tt);
xPost = 0;
pPost = Q;
for i = 1:tt
    % predykcja
    xPrio = xPost;
    pPrio = pPost + Q;
    
    % filtracja
    K = pPrio / (pPrio + R);
    xPost = xPrio + K * (y(i) - xPrio);
    pPost = (1 - K) * pPrio;
    
    xHat(i) = xPost;
end

figure;
plot(t,y,'b'); hold on; grid on;
plot(t,xHat,'r');
legend('wyjscie','estymata');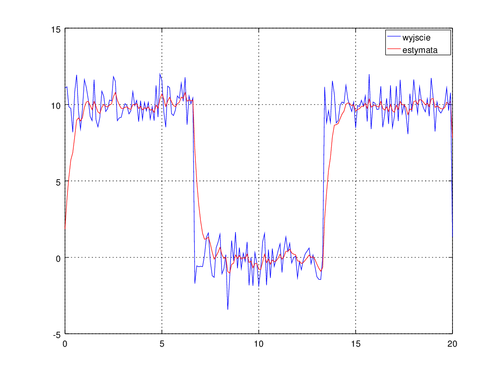

Przykład 2. Równania ruchu.

Sztandarowym przykładem wykorzystania FK jest estymacja stanu ruchu obiektu. Dotyczy to zarówno ruchu liniowego jak i obrotowego, w jednym lub wielu wymiarach. Prócz odszumiania danych pochodzących z GPSu, żyroskopu czy akcelerometru, FK pozwala na fuzję danych z wielu czujników równocześnie w celu poprawy ostatecznej oceny stanu. Warto więc wyprowadzić model poruszającego się obiektu (zakładając póki co tylko jeden wymiar) bo można się na niego natknąć niemalże wszędzie.

Do opisu poruszającego się obiektu w jednym wymiarze przyjmuje się następujący wektor stanu: $$ x=\begin{bmatrix}s & v & a\end{bmatrix}^T, $$ gdzie elementy wektora $x$ to kolejno droga, prędkość i przyspieszenie. Korzystając ze wzorów: $$ s=vt+\frac{at^2}{2}, \quad \frac{ds}{dt}=v, \quad \frac{dv}{dt}=a, $$ oraz dokonując ich dyskretyzacji: $$ s_{k+1}=s_k+hv_k+\frac{h^2}{2}a_k,\\ v_{k+1}=v_{k}+ha_k,\\ a_{k+1}=a_k, $$ otrzymujemy model ruchu prostoliniowego w postaci: $$ \begin{bmatrix}s_{k+1} \\ v_{k+1} \\ a_{k+1}\end{bmatrix} = \begin{bmatrix} 1 & h & \frac{h^2}{2} \\ 0 & 1 & h\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}s_k \\ v_k \\ a_k\end{bmatrix}. $$ Powyższy model jest jeszcze wybrakowany ponieważ brakuje w nim uwzględnienia zakłóceń stanu oraz równania wyjścia. Te z kolei zależą od postawionego przed filtrem zadania. Wspomniany model nie posiada wejść. Załóżmy, że z użyciem odpowiednich urządzeń pomiarowych mierzone są przyspieszenie i prędkość pewnego ciała. Zadaniem FK jest fuzja obydwu sygnałów w celu odtworzenia położenia ciała oraz odszumienie zebranych pomiarów. Uwzględniając zatem obecność dwóch składowych stanu będących obciążonymi zakłóceniami, wprowadzamy zależności: $$ v_k=\tilde{v}_k+w^v_k, \quad a_k=\tilde{a}_k+w^a_k, $$ gdzie: $w^v_k$ - zakłócenie prędkości, $w^a_k$ - zakłócenie przyspieszenia. Uzupełniając model powyższymi równaniami otrzymuje się: $$ \begin{bmatrix}s_{k+1} \\ v_{k+1} \\ a_{k+1}\end{bmatrix}_{x_{k+1}} = \begin{bmatrix} 1 & h & \frac{h^2}{2} \\ 0 & 1 & h\\ 0 & 0 & 1 \end{bmatrix}_A \begin{bmatrix}s_k \\ v_k \\ a_k\end{bmatrix}_{x_k} + \begin{bmatrix} h & \frac{h^2}{2} \\ 1 & h \\ 0 & 1 \end{bmatrix}_q \begin{bmatrix} w^v_k \\ w^a_k \end{bmatrix}_{w_k}. $$ Biorąc pod uwagę, że pomiarowo dostępne są prędkość oraz przyspieszenie, wyprowadzamy równanie wyjścia: $$ \begin{bmatrix} y^v_k \\ y^a_k \end{bmatrix}_{y_k} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}_H \begin{bmatrix}s_k \\ v_k \\ a_k\end{bmatrix}_{x_k} + \begin{bmatrix} v^v_k \\ v^a_k \end{bmatrix}_{v_k}. $$ Indeksy dolne macierzy oznaczają macierze modelu FK. Macierz wejścia $B$ jest równa 0. Macierz kowariancji szumu pomiarowego, przy założeniu braku korelacji pomiędzy zakłóceniami dana jest w postaci: $$ R = \begin{bmatrix} \sigma^2_v & 0 \\ 0 & \sigma^2_a \end{bmatrix}, $$ gdzie: $\sigma^2_v$ - wariancja pomiaru prędkości, $\sigma^2_a$ - wariancja pomiaru przyspieszenia. Macierz kowariancji szumu procesowego przedstawia się następująco: $$ Q = q \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \alpha \right)_W q^T, $$ gdzie: $\alpha$ to doświadczalnie dobrany parametr w zależności od pożądanych cech filtra. Tradycyjnie implementacja i przykładowy wynik działania skryptu przedstawiono poniżej:

Plik: kalman2.m

tSim = 10;
h = 0.01;
t = 0:h:tSim;
tt = numel(t);

% przyspieszenie teoretyczne
a = square(t, 1/tSim,20) * 5 - 2;

% predkosc teoretyczna
v = zeros(1,tt);
for i = 1:(tt-1)
   v(i+1) = v(i) + h * a(i);
end

% zaszumienie wartosci teoretycznych
sigma_a = 0.5;
as = a + sigma_a * randn(1,tt);
sigma_v = 1;
vs = v + sigma_v * randn(1,tt);

% droga wynikajaca z modelu
s = zeros(1,tt);
for i = 1:(tt-1)
    s(i+1) = s(i) + h * v(i) + h^2/2 * a(i);
end

% macierz pomiarow
y = [vs;as];

% model FK
A = [1 h h^2/2;
    0 1 h;
    0 0 1];
B = 0;
H = [0 1 0;
    0 0 1];
R = [sigma_v^2 0;
    0 sigma_a^2];
q = [h h^2/2;
    1 h;
    0 1];
W = eye(2) * 0.002;

% FK
xHat = zeros(3,tt);
xPost = zeros(3,1);
Ppost = zeros(3,3);
I = eye(3);
for i = 1:tt
    [xPost,Ppost] = KalmanFilter(A,B,H,q,W,R,0,y(:,i),xPost,Ppost,h);
    xHat(:,i) = xPost;
end

% wyniki
figure;
subplot(3,1,1);
plot(t,a,'g');hold on;grid on;
plot(t,as,'r');
plot(t,xHat(3,:),'b');
legend('wzor','pomiar','estymata');
title('przyspieszenie');
subplot(3,1,2);
plot(t,v,'g');hold on;grid on;
plot(t,vs,'r');
plot(t,xHat(2,:),'b');
legend('wzor','pomiar','estymata');
title('predkosc');
subplot(3,1,3);
plot(t,s,'g');hold on;grid on;
plot(t,xHat(1,:),'b');
legend('wzor','estymata');
title('przemieszczenie');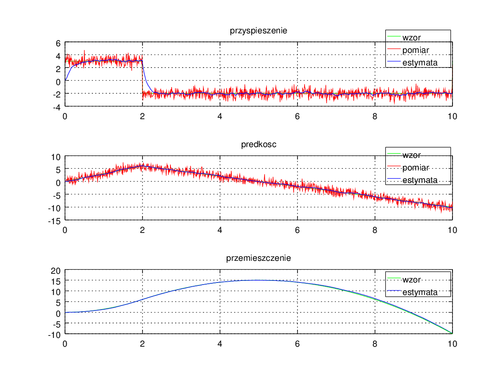

Przykład 3. Układ RLC.

Ostatnim przykładem, który jest moim zdaniem warty rozpatrzenia jest badanie działania układu RLC. Zadanie jest o tyle ciekawe, że w pierwszej kolejności zostanie wyznaczony model matematyczny w postaci liniowych równań różniczkowych, zostanie dokonana dyskretyzacja równań oraz kompozycja modelu do FK. Zakładamy, że mierzone jest napięcie na kondensatorze czwórnika RLC, które obarczone jest szumami pomiarowymi. Zadaniem FK będzie prócz filtracji napięcia, odtworzenie drugiego elementu wektora stanu - prądu cewki, a w zasadzie prądu w całym układzie.

Klasyczny czwórnik RLC przedstawia się następująco: 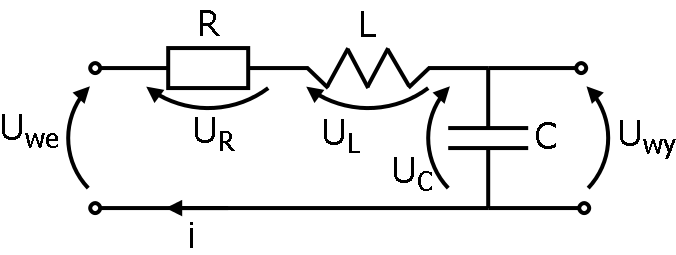gdzie: $U_{we}$ - napięcie wejściowe, $U_{wy}$ - napięcie wyjściowe, $U_x$ - spadek napięcia na poszczególnych elementach obwodu, $i$ - prąd układu. Model matematyczny można wyprowadzić korzystając z II prawa Kirchoffa: $$ U_{we}=U_R+U_L+U_C\\ U_{wy}=U_C, $$ oraz zależności wiążących prądy i napięcia płynące przez elementy bierne: $$ U_R=Ri, \quad U_L=L\frac{di}{dt}, \quad i=C\frac{dU_c}{dt}. $$ Jako elementy wektora stanu najwygodniej jest przyjąć wielkości występujące w powyższych zależnościach w postaci pochodnych stąd wektor stanu dany jest jako: $$ x=\begin{bmatrix}i & U_C\end{bmatrix}^T. $$ Ostatecznie model matematyczny po podstawieniu wszystkich zależności i przekształceniu do postaci równań stanu przedstawia się następująco: $$ \frac{d}{dt}\begin{bmatrix} i \\ U_C \end{bmatrix}_{\dot{x}} = \begin{bmatrix} -\frac{R}{L} & -\frac{1}{L} \\ \frac{1}{C} & 0 \end{bmatrix}_{A} \begin{bmatrix} i \\ U_C \end{bmatrix}_{x} + \begin{bmatrix} \frac{1}{L} \\ 0 \end{bmatrix}_{B} U_{We} \\ y= \begin{bmatrix} 0 & 1 \end{bmatrix}_{C} \begin{bmatrix} i \\ U_C \end{bmatrix}_{x}. $$ Aby możliwe było użycie powyższego modelu w filtrze Kalmana należy dokonać dyskretyzacji powyższych równań. Na chwilę obecną pomijane jest uwzględnienie zakłóceń stanu. Zostaną one ujęte dopiero w modelu dyskretnym. Dokonując dyskretyzacji modelu ciągłego, przy założeniu stałości wejścia pomiędzy okresami próbkowania (użycie ekstrapolatora zerowego rzędu dla wejścia układu) otrzymuje się równania ogólne: $$ x_{k+1}=A_dx_k+B_du_k\\ y_k=H_dx_k, $$ gdzie macierze z indeksem dolnym $d$ oznaczają macierze układu dyskretnego dane w postaci: $$ A_d=e^{Ah}, \quad B_d=A^{-1}\left(e^{Ah}-I\right)B, \quad H_d=C, $$ gdzie: $h$ - okres próbkowania. Macierz $e^X$ dana jest w postaci szeregu: $$ e^X=\sum_{k=0}^{\infty}{\frac{1}{k!}X^k}. $$ W praktyce eksponentę macierzy wyznacza się w bardziej efektywny numerycznie sposób. Dla zadania dyskretyzacji można się pokusić o przybliżenie wyrażenia $e^{Ah}$:

• $e^{Ah}\approx I+Ah$ - metoda najprostsza, odpowiadająca przybliżeniu pochodnej: $\frac{dx}{dt}\approx \frac{x_{k+1}-x_k}{h}$. Jej wadą jest możliwa niestabilność układu dyskretnego pomimo stabilności układu ciągłego z powodu zbyt dużej wartości okresu próbkowania.
• $e^{Ah}\approx \left(I-Ah\right)^{-1}$
• $e^{Ah}\approx \left(I+0.5Ah\right)\left(I-0.5Ah\right)^{-1}$ - znane jako podstawienie Tustina: $$ s=\frac{2}{h}\frac{z-1}{z+1}, $$ transformujące przestrzeń Laplace'a do przestrzeni Z.

Model dyskretny układu należy dodatkowo uzupełnić o informacje mówiące o zakłóceniach stanu. Jedyną wielkością mierzoną jest napięcie $U_C$, dlatego wstawiając zależność $U_{C_k}=\tilde{U}_{C_k}+w^U_{C_k}$ do zdyskretyzowanego modelu oraz uwzględniając zakłócenie pomiaru otrzymujemy ostatecznie: $$ x_{k+1}=A_dx_k+B_du_k + \begin{bmatrix} a_{12} \\ 0 \end{bmatrix}_{q} w^{U_C}_k \\ y_k=H_dx_k+v^{U_C}_k, $$ gdzie: $a_{12}$ - element pierwszego wiersza, drugiej kolumny zdyskretyzowanej macierzy $A_d$. Wszystkie powyższe działania zostały zaimplementowane w poniższym skrypcie:

Plik: kalman3.m

clear all;

tSim = 25;
dt = 0.01;
t = 0:dt:tSim;
tt = numel(t);

% dwa okresy sygnalu prostokatnego jako wejscie
u = square(t,1/tSim*2,50);

% parametry ukladu
R = 20;
L = 10;
C1 = 0.01;

% macierze ukladu
A = [-R/L -1/L;
    1/C1 0];
B = [1/L;
    0];
C = [1, 0;
    0, 1];
    
q = [-1/L;
    0];

% symulacja ukladu ciaglego z uzyciem RK4
x_0 = [0;0];
x_c = zeros(2,tt);
y_c = zeros(2,tt);
ss_hndl = @(A,B,state,u) (A * state + B * u);
out_hndl = @(C,state) (C * state);
x_c(:,1) = x_0;
y_c(:,1) = out_hndl(C,x_0);
for i = 2:tt
    k1 = dt * ss_hndl(A,B,x_c(:,i-1), u(i));
    k2 = dt * ss_hndl(A,B,x_c(:,i-1) + 0.5 * k1, u(i));
    k3 = dt * ss_hndl(A,B,x_c(:,i-1) + 0.5 * k2, u(i));
    k4 = dt * ss_hndl(A,B,x_c(:,i-1) + k3, u(i));
    x_c(:,i) = x_c(:,i-1) + 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4);
    y_c(:,i) = out_hndl(C,x_c(:,i));
end

% dyskretyzacja
I = diag(ones(size(A,1),1));
%eat = expm(A * dt);
%eat = A + I * dt;
eat = (I + 0.5 * A * dt) * (I - 0.5 * A * dt)^-1;
A_d = eat;
B_d = A^-1 * (eat - I) * B;
C_d = C;

% symulacja ukladu dyskretnego
x_d = zeros(size(A,1),tt);
y_d = zeros(size(A,1),tt);
for i = 1:tt
    if i == 1
        x_d(:,i) = x_0;
    else
        x_d(:,i) = A_d * x_d(:,i-1) + B_d * u(i);
    end
    y_d(:,i) = C_d * x_d(:,i);
end

% porownanie ukladu ciaglego i dyskretnego
figure;
subplot(2,1,1);
plot(t,y_c(1,:),'r',t,y_d(1,:),'b'); grid on;
title('i');
legend('ciagly','dyskretny');
subplot(2,1,2);
plot(t,y_c(2,:),'r',t,y_d(2,:),'b'); grid on;
title('Uc');
legend('ciagly','dyskretny');

% zaklocenia wyjscia w ukladzie dyskretnym
sigma_uc = 0.1;
y_d(2,:) = y_d(2,:) + randn(1,tt) * sigma_uc;

% FK
x_p = zeros(2,tt);
x_prio = zeros(2,1);
x_post = [0; 0];
P_prio = zeros(2,2);
P_post = zeros(2,2);

A_k = A_d;
B_k = B_d;
H_k = [0,1];
q_k = [A_k(1,2);0];
W = 0.01;
R = sigma_uc^2;

xHat = zeros(2,tt);
xPost = zeros(2,1);
Ppost = zeros(2,2);
for i = 1:tt
    [xPost,Ppost] = KalmanFilter(A_k,B_k,H_k,q_k,W,R,u(i),y_d(2,i),xPost,Ppost,dt);
    xHat(:,i) = xPost;   
end

% wyniki dzialania FK
figure;
subplot(2,1,1);
plot(t,x_d(1,:),'g',t,xHat(1,:),'b'); grid on;
title('i');
legend('wzor','estymata');
subplot(2,1,2);
plot(t,y_d(2,:),'r',t,x_d(2,:),'g',t,xHat(2,:),'b'); grid on;
title('uc');
legend('pomiary','wzor','estymata');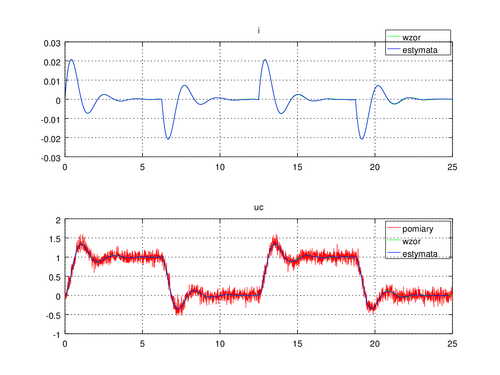

Przykład 4. Ruch ciała w 2D. Symulator.

Pomysł na stworzenie jakiegoś przykładu realizacji FK w przeglądarce zaczerpnąłem stąd: Forbot.pl - Filtr Kalmana w praktyce – 3 przykłady z kodami!, gdzie Autor prezentuje wykorzystanie FK do estymacji położenia kursora (implementacja w OpenCV). Postanowiłem odtworzyć ten pomysł z użyciem jQuery oraz obiektu canvas wprowadzonym wraz z HTML5. Przykład jest zarówno w sporym stopniu "interaktywny" jak i prosty na tyle, aby prezentował niezerową wartość edykacyjną. Pozwoliłem sobie też na kilka zmian, moim zdaniem istotnych:

• Użytkownik rysuje trasę kursora (kolor zielony), która dodatkowo zakłócana jest szumem (obydwie składowe, kolor czerwony), zaś estymata wyznaczana jest z nieco innego, okrojonego modelu (kolor niebieski).
• Przyjęty przeze mnie model jest uproszczony (taki jak w przykładzie 1) w stosunku do tego z artykułu, który dodatkowo uwzględnia prędkość kursora. Trudno też zgodzić mi się z tym, jakoby rozbudowa modelu o przyspieszenie miałaby dodatkowo polepszyć śledzenie kursora. Model FK dany jest jako: $$ \begin{bmatrix} s^x_{k+1} \\ s^y_{k+1} \end{bmatrix}_{x_{k+1}} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}_{A} \begin{bmatrix} s^x_{k} \\ s^y_{k} \end{bmatrix}_{x_{k}} + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}_{q} \begin{bmatrix} w^x_{k} \\ w^y_{k} \end{bmatrix}_{w_{k}} $$
• Macierze $Q$ i $R$ dobrane są przeze mnie w sposób taki, jaki omawiany był w przykładach teoretycznych jednak z racji prostego modelu upraszczają się one do postaci: $$ Q=I\alpha, \quad R=I \sigma_{x,y}, $$ gdzie: $\sigma_{x,y}$ - odchylenie standardowe zakłócenia pomiaru położenia kursora dla obydwu składowych.

Symulator udostępnia możliwość zmiany dwóch parametrów: zakłócenia położenia $\sigma_{x,y}$ oraz parametr strojenia FK $\alpha$. Warto sprawdzić działanie filtru w zależności od wartości tego drugiego. Całość implementacji znajduje się w pliku: kalman.js.

Wykorzystane narzędzia.

• Octave - środowisko obliczeniowe, darmowy odpowiednik Matlaba,
• mathjs - biblioteka matematyczna w JavaScripcie użyta w symulatorze,
• MathJax - LaTeXowe formuły matematyczne w przeglądarce,
• highlight.js - lekka biblioteczka do podświetlania składni kodu.

Warte przeczytania źródła.

• Artykuły z Forbot.pl: Filtr Kalmana od teorii do praktyki – #1 – Matlab oraz Filtr Kalmana w praktyce – 3 przykłady z kodami!.
• Nieśmiertelna Wiki: Kalman_filter.
• Publikacja: Wyznaczanie orientacji obiektu w przestrzeni z wykorzystaniem naiwnego filtru Kalmana, autorzy: Robert Bieda, Rafał Grygiel, Politechnika Śląska w Gliwicach (moim zdaniem świetni dydaktycy, publikacja jest naprawdę warta przeczytania).