Transformacja PCA

Wstęp.

Niedawno miałem okazję zapoznać się z tytułową transformacją PCA (Principal Component Analysis). Biorąc pod uwagę, że temat jest dosyć ciekawy i prosty, a wynikowe skrypty zwięzłe i proste w zrozumieniu, postanowiłem opisać temat, może komuś się przyda.

Transformacja PCA jest algorytmem analizy danych. Wykorzystuje w tym celu informacje dotyczące powiązań pomiędzy danymi wejściowymi. Umożliwia to dokonanie selekcji i "kompresji" danych bez utraty istotnych informacji pierwotnego zestawu danych. Stąd wniosek, że PCA może być wykorzystane właśnie w problemach kompresji, analizy oraz przetwarzania złożonych zbiorów danych tak, aby wyłuszczyć z nich składaniki o największej zmienności i największym wpływie na pozostałe informacje. Pozwala na zredukowanie problemu analizy N zmiennych/składników/parametrów do problemu K wymiarowego przy czym: $$ K < N. $$ Sama transformacja jest przekształceniem liniowym danym w postaci: $$ \mb{Y}=\mb{W} \mb{X}, $$ gdzie: $\mb{Y}$ - macierzą przestrzeni wyjściowej, zachowującej najistotniejsze informacje danych wejściowych $\mb{X}$. Macierz $\mb{W}$ jest macierzą przekształcenia PCA.

W ramach tego opracowania zostanie przedstawiony kompletny algorytm transformacji PCA, który zostanie wykorzystany do rozwiązania kilku przykładowych problemów.

Wstęp teoretyczny.

Nie ma nic bardziej praktycznego niż dobra teoria więc wypadałoby zacząć od krótkiego wstępu teoretycznego oraz określenia wszystkich wielkości, które będą niezbędne do ożywienia transformacji PCA.

Niech dany jest wektor cech/zmiennych/pomiarów o długości $N$: $$ \mb{x}=\left[x_1, x_2, ... , x_N\right]^T, $$ który traktowany jest jako pojedynczy pomiar/obserwacja. Zbiór danych wejściowych algorytmu PCA dla $P$ obserwacji dany jest w postaci: $$ \mb{X}=\left[\mb{x_1}, \mb{x_2}, ... ,\mb{x_P}\right]. $$ Jak nietrudno zauważyć, macierz danych wejściowych ma rozmiar $N\times P$, gdzie ilość wierszy odpowiada ilości zmiennych zaś liczba kolumn ilości obserwacji/realizacji danych zmiennych. Dla tak przygotowanych danych należy wyznaczyć macierz autokorelacji (przy założeniu, że wartość oczekiwana zmiennych jest równa zero): $$ \mb{R_{xx}}=\frac{1}{P}\mb{X}\mb{X}^T. $$ Macierz $\mb{R_{xx}}$ posiada wymiary $N\times N$. W skrócie macierz ta informuje o tym w jakim stopniu uzyskane dane są ze sobą skorelowane. Kolejnym krokiem algorytmu jest wyznaczenie wartości własnych macierzy $\mb{R_{xx}}$ oraz odpowiadających im wektorów własnych. Wartości te, wraz z odpowiadającymi im wektorami własnymi należy uszeregować malejąco. W ten sposób uzyskuje się macierz diagonalną: $$ \mb{D}=\begin{bmatrix} \lambda_1 & 0 & \ldots & 0\\ 0 & \lambda_2 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \ldots & \lambda_N \end{bmatrix} $$ gdzie: $\lambda_1 > \lambda_2 > ... > \lambda_N$ to wartości własne oraz której odpowiada macierz wektorów własnych: $$ \mb{V}=\left[\mb{v}_1, \mb{v}_2, ... , \mb{v}_N\right]. $$ Istotnym krokiem transformacji jest ocena ile najistotniejszych czynników należy uwzględnić w przekształceniu. W tym celu należy wybrać pierwszy $K$ największych wartości własnych macierzy $\mb{L}$, odstających znacząco od pozostałych. W ten sposób sposób uzyskuje się macierz diagonalną o zredukowanej ilości wartości własnych: $$ \mb{L}=\begin{bmatrix} \lambda_1 & 0 & \ldots & 0\\ 0 & \lambda_2 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \ldots & \lambda_K \end{bmatrix} $$ oraz macierz przekształcenia $\mb{W}$ uwzględniającą $K$ znaczących wektorów własnych (transponowanych): $$ \mb{W}=\left[ \mb{v}_1, \mb{v}_2, ... , \mb{v}_N\right]^T. $$ Macierz $\mb{W}$ posiada wymiary $K\times N$ Ostatecznie przekształcenie PCA dla kompletnego zbioru danych wejściowych prezentuje się jak przedstawiono we wstępie: $$ \mb{Y}=\mb{W} \mb{X}. $$ Jak nietrudno zauważyć, macierz $\mb{Y}$ ma wymiary $K\times P$. Istotnym elementem analizy wpływu ilości uwzględnionych składników głównych jest błąd wynikający z różnicy pomiędzy macierzą autokorelacji, a macierzą zdekomponowaną danej w postaci: $$ \mb{\hat{R}_{xx}}\cong \mb{W}^T L\mb{W}. $$ Aby odtworzyć macierz danych wejściowych należy skorzystać z przekształcenia: $$ \hat{\mb{X}}=\mb{W}^T \mb{Y}. $$ Istotną kwestią w kontekście przedstawionego problemu jest normalizacja danych wejściowych. Aby uniknąć sytuacji, kiedy wyniki transformacji uzależnione będą rzędów wielkości dla poszczególnych zmiennych warto zastosować jedną z metod normalizacji: $$ \mb{X}_{norm}=\mb{X} - \mb{X}_{mean}, \mb{X}_{norm}=\frac{\mb{X}}{\mb{X}_{max}}, \mb{X}_{norm}=\frac{\mb{X} - \mb{X}_{mean}}{\sigma_\mb{X}}, $$ gdzie: $\mb{X}_{mean}$ - wartość średnia dla danej zmiennej w zestawie danych, $\mb{X}_{max}$ - wartość maksymalna, $\sigma_\mb{X}$ - odchylenie standardowe danej zmiennej dla wszystkich obserwacji $P$. Dla uściślenia: wartości średnie, maksymalne i odchylenia liczone są dla każdej kolmny danych (zmiennej) z osobna.

Przykład I - zadanie syntetyczne.

Na pierwszy ogień idzie prosty przykład syntetyczny, który ma na celu wyjaśnienie jak stosować transformację PCA, krok po kroku. Z tej okazji wygenerowano macierz danych w postaci:

Obserwacja	$x_1$	$x_2$	$x_3$
1	2	1	3
2	3	0	2
3	1	3	1
4	4	4	0

Jak można zauważyć, macierz danych wejściowych zawiera $N=3$ zmienne oraz $P=4$ pomiarów. Do dalszych obliczeń należy dokonać transponowania zestawu danych. Macierz autokorelacji jest równa: $$ \mb{R}_{xx}=\begin{bmatrix} 7.5 & 5.25 & 3.25\\ 5.25 & 6.5 & 1.5\\ 3.25 & 1.5 & 3.5\\ \end{bmatrix}. $$ Macierz diagonalna z posortowanymi wartościami własnymi wraz z uszeregowanymi wektorami własnymi przedstawiają się następująco: $$ \mb{D} = \begin{bmatrix} 13.4560 & 0 & 0\\ 0 & 3.0849 & 0\\ 0 & 0 & 0.9591\\ \end{bmatrix}, \mb{V} = \begin{bmatrix} -0.6673 & 0.1943 & 0.7190\\ 0.4775 & -0.6293 & 0.6132\\ 0.5716 & 0.7525 & 0.3271\\ \end{bmatrix}. $$ Jak widać, dla zestawu danych nie da się wyróżnić jednej, dominującej wartości własnej macierzy autokorelacji. Dla $K=3$ składowych głównych (dla wszystkich składowych wejściowych), uzyskuje się macierz przekształcenia PCA: $$ \mb{W} = \begin{bmatrix} 0.7190 & 0.6132 & 0.3271\\ 0.1943 & -0.6293 & 0.7525\\ -0.6673 & 0.4775 & 0.5716\\ \end{bmatrix}, $$ która pozwala na odtworzenie macierzy autokorelacji bezbłędnie: $$ \varepsilon_{R}=\left|\left|\mb{R}_{xx}-\hat{\mb{R}}_{xx}\right|\right|=0. $$ Przekształcenie PCA ma ostatecznie postać: $$ \mb{Y}= \begin{bmatrix} 3.0325 & 2.8112 & 2.8857 & 5.3289\\ 2.0169 & 2.0880 & -0.9409 & -1.7397\\ 0.8578 & -0.8586 & 1.3368 & -0.7591\\ \end{bmatrix}, $$ zaś odwrotna transformacja skutkuje bezstratnym odtworzeniem danych wejściowych: $$ \varepsilon_{X}=\left|\left|\mb{X}-\hat{\mb{X}}\right|\right|=0. $$ Przeprowadźmy jeszcze te same obliczenia ale pomijając jeden, najmniej znaczący składnik. Wybieramy zatem $K=2$ składowych głównych i uzyskujemy: $$ \mb{W} = \begin{bmatrix} 0.7190 & 0.6132 & 0.3271\\ 0.1943 & -0.6293 & 0.7525\\ \end{bmatrix}, \mb{Y}= \begin{bmatrix} 3.0325 & 2.8112 & 2.8857 & 5.3289\\ 2.0169 & 2.0880 & -0.9409 & -1.7397\\ \end{bmatrix}, $$ $$ \hat{\mb{R}}_{xx} = \begin{bmatrix} 7.0730 & 5.5556 & 3.6158\\ 5.5556 & 6.2813 & 1.2382\\ 3.6158 & 1.2382 & 3.1866\\ \end{bmatrix}, \hat{\mb{X}}=\begin{bmatrix} 2.5724 & 2.4271 & 1.8920 & 3.4935\\ 0.5904 & 0.4100 & 2.3617 & 4.3625\\ 2.5097 & 2.4908 & 0.2359 & 0.4339\\ \end{bmatrix}. $$ Błędy odtworzeń dla zmniejszonej przestrzeni wynoszą: $$ \varepsilon_{\mb{R}} = 0.9591, \varepsilon_{\mb{X}} = 1.9587, $$ zaś błędy względne wynoszą odpowiednio $0.0713$ oraz $0.2670$ co oznacza istotny ubytek użytecznych informacji pierwotnego zestawu danych. Do wygenerowanie powyższych wyników wykorzystano poniższy skrypt:

Plik: pca_sample.m

clear all;
clc;

% dane wejsciowe, P=4 - ilosc obserwacji, N=3 - ilosc zmiennych
X = [2, 1, 3;
    3, 0, 2;
    1, 3, 1;
    4, 4, 0];

P = size(X, 1); %ilosc obserwacji

% transponowanie danych
X = X'; %3x4

% macierz korelacji
R = (X * (X')) / P; %3x3

% wartosci wlasne i wektory wlasne macierzy korelacji - posortowane
% malejaco
[V,D] = eig(R);
[d,I] = sort(diag(D), 'descend');
D = diag(d);
V_sorted = V(:, I); %3x3

K = 2; % ilosc skladnikow glownych

W = (V_sorted (:, 1:K))'; %2x3

% odtworzenie macierzy korelacji
L = diag (d (1:K)); %2x2
R_hat = W' * L * W; %3x2 * 2x2 * 2x3 = 3x3

% transformacja PCA
Y = W * X; % 2x3 * 3x4 = 2x4

% odtworzenie danych wejsciowych
X_hat = W' * Y; % 3x2 * 2x4 = 3x4

% bledy odtworzen
er = norm (R - R_hat) % bezwzgledny
der = er / norm (R) % wzgledny
ex = norm (X - X_hat)
dex = ex / norm (X)

Przykład II - transformacja funkcji.

Jako kolejny przykład warto przeanalizować to jak zachowuje się transformacja PCA przy przetwarzaniu danych będących wartościami funkcji. Na tę okazję przygotowałem funkcję implementującą obliczenia ze wcześniejszego skyptu:

Plik: pca_transform.m

function [ Y, W, R, R_hat, X_hat ] = pca_transform( X, K )
    P = size(X, 2); %ilosc obserwacji - kolumn, ilosc zmiennych N - wierszy
    N = size(X, 1);

    % macierz korelacji
    R = (X * (X')) / P; %3x3

    % wartosci wlasne i wektory wlasne macierzy korelacji - posortowane
    % malejaco
    [V,D] = eig(R);
    [d,I] = sort(diag(D), 'descend');
    V_sorted = V(:, I); %3x3

    W = (V_sorted (:, 1:K))'; %2x3

    % odtworzenie macierzy korelacji
    L = diag (d (1:K)); %2x2
    R_hat = W' * L * W; %3x2 * 2x2 * 2x3 = 3x3

    % disp ('Macierz wartosci wlasnych: '); diag(d)
    % disp ('Macierz wektorow wlasnych: '); V_sorted
    
    % transformacja PCA
    Y = W * X; % 2x3 * 3x4 = 2x4

    % odtworzenie danych wejsciowych
    X_hat = W' * Y; % 3x2 * 2x4 = 3x4
end

Jak nietrudno się domyślić, argumentami funkcji jest zbiór danych (wiersze - zmienne, obserwacje - kolumny) oraz ilość uwzględniadnych składowych. Jako skrypt uruchamiający użyto:

Plik: pca_sample2.m

clear all;
clc;

t = 0:0.1:2*pi;
X = [sin(t)', cos(t)', (exp(-0.4*t) .* sin(t))', 0.5 * randn(numel(t),1)];

figure;
plot (X);

X = X';
[ Y, W, R, R_hat, X_hat ] = pca_transform( X, 4);

figure;
plot (X_hat');


% bledy odtworzen
er = norm (R - R_hat) % bezwzgledny
der = er / norm (R) % wzgledny
ex = norm (X - X_hat)
dex = ex / norm (X)

Zbiorem danych są 4 wektory kolumnowe z kolejnymi funkcjami, w tym jedną generującą liczby pseudolosowe. Dla takiego przeblemu uzyskano następujące wyniki transformacji:

Oryginał	Po transformacji
K=4

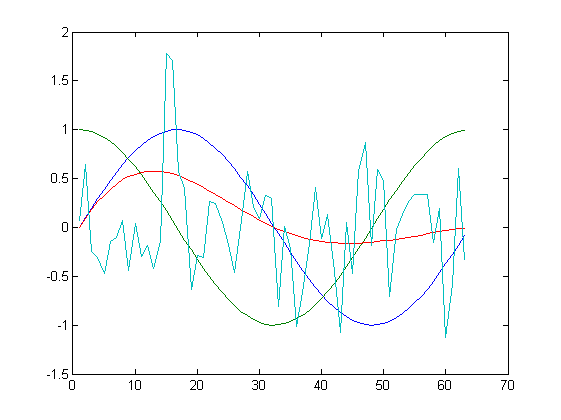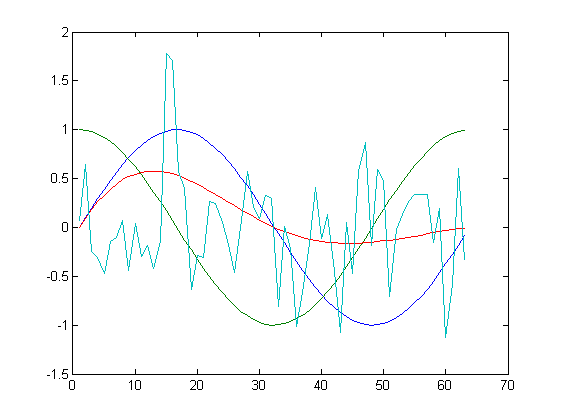K=3

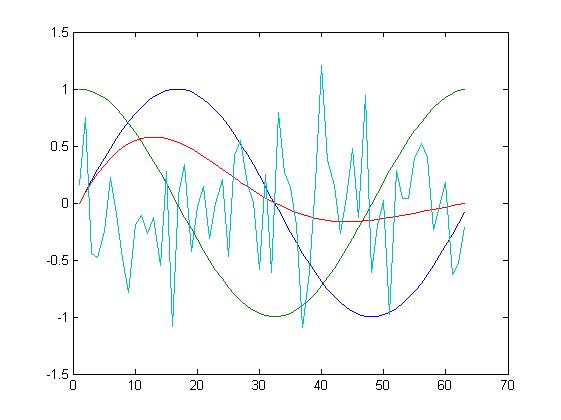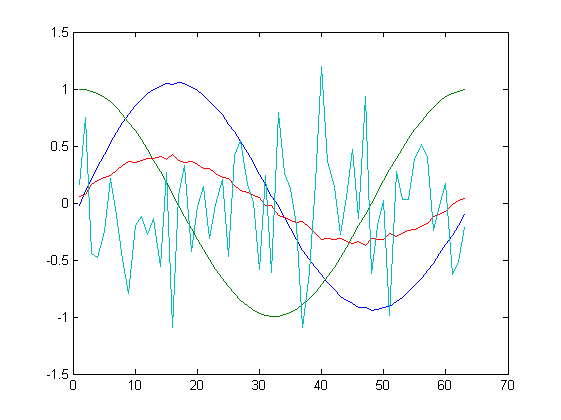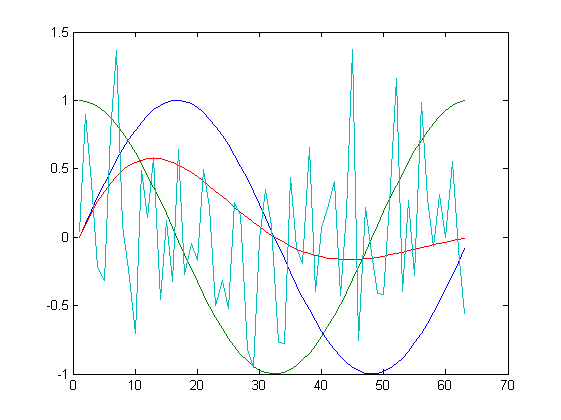
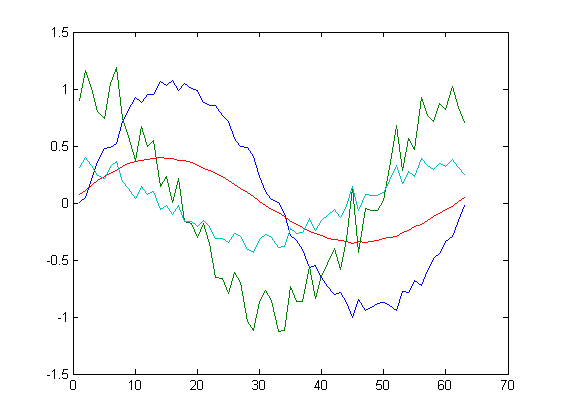
K=2

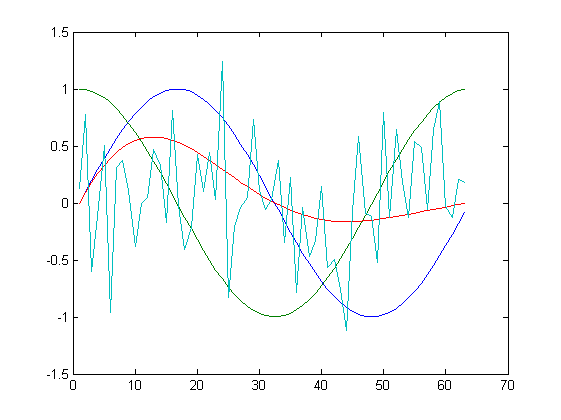
K=1

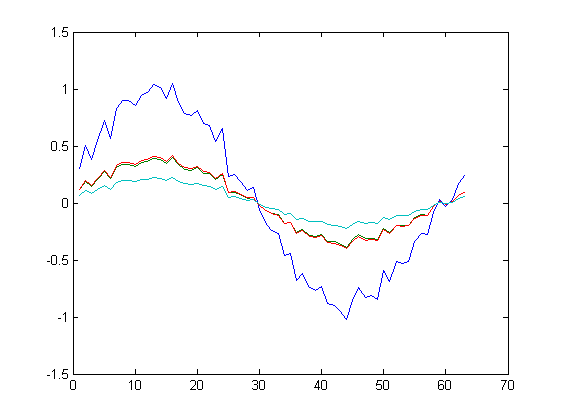Jak widać na powyższych rysunkach, przy uwzględnienia wszystkich składowych, algorytm odtwarza funkcje bezbłędnie. Dla $K=3$ bezbłędnie odtworzony jest przebieg losowy oraz funkcje $e^{-0.4t}sin(t)$. W pozostałych dwóch funkcjach widoczne są już zniekształcenia. Dla $K=2$ oraz $K=1$ następuje znacząca kompresja danych, tylko kształt funkcji $sin$ oraz $cos$ są odwzorowane w nieco większym stopniu.

Warto rzucić okiem na wartości własne jakie można uzyskać w trakcie działania skryptu: $$ d=\left[0.5706, 0.5066, 0.2350, 0.0169\right]^T. $$ Jedna z wartości własnych jest zdecydowanie mniejsza od pozostałych i to jej można się bez znaczącej utraty informacji pozbyć. Dalsze ucinanie składowych powoduje już znaczące trudności w odtworzeniu oryginalnego zestawu danych.

Przykład III - transformacja obrazu.

Kolejnym przykładem wartym rozpatrzenia jest zastosowanie transformacji PCA do kompresji obrazów. W tym celu przygotowałem prosty skrypt, który wczytuje obraz, dzieli go na kwadraty 32x32 piksele oraz dla każdego kwadratu przeprowadza trasformację PCA oraz przekształcenie odwrotne. Odpowiada to przetwarzaniu partia po partii zbioru danych dla $N=32$ składowe oraz $P=32$ obserwacje. Za obraz testowy użyto nieśmiertelnego obrazu Leny (256x256 pikseli, 8 bitowa paleta odcieni szarości):

Skrypt użyty do przeprowadzenia badania przedstawia się następująco:

Plik: pca_sample3.m

clear all;
clc;

lena = imread('lena.png');

window_size = 32;

width = size(lena, 2);
height = size(lena, 1);

windows_per_width = width / window_size;
windows_per_height = height / window_size;

output = zeros(height, width);

K = 16;

for i = 1:windows_per_height
    for j = 1:windows_per_width
        ind1 = ((i-1) * window_size + 1):(i * window_size);
        ind2 = ((j-1) * window_size + 1):(j * window_size);
        window = lena (ind1, ind2);
        [Y, W, R, R_hat, window_new] = pca_transform(double(window), K);
        
        output(ind1, ind2) = window_new;
    end
end

output = uint8(output);

figure;
imshow(output);
imwrite(output, ['lenak', num2str(K),'.png']);

mse = 1 / (width * height) * sum(sum((lena - output).^2))
psnr = 20 * log10(255) - 10 * log10(mse)

Badania przeprowadzono dla kilku wartości najistotniejszych składowych:

$K=1$	$K=2$

$K=4$	$K=8$

$K=16$

Pora na kilka wniosków. Na obrazkach z mniejszą ilością głównych składowych widać wyraźnie miejsca "cięcia" obrazów. Warto również sprawdzić wartości wskaźników MSE oraz PSNR. Dla $K=32$ błąd średniokwadratowy wynosi 0 zaś odstęp od szumu jest nieskończony. Na podstawie powyższej tabeli łatwo stwierdzić, że już dla $K=8$ obraz prezentuje się całkiem dobrze. Dla $K=16$ jest już nieodróżnialny od oryginału.

Przykład IV - płaszczyzna PCA.

Jako przykład ostatni weźmy po lupę pewien zestaw danych statystycznych (wybrane dane GUS dotyczące miast wojewódzkich) określających poziom zamożności. Wzięte zostaną pod uwagę cztery parametry: $x_1$ - bezrobocie zarejestrowane [%], $x_2$ - przeciętne miesięczne wynagrodzenie brutto w sektorze przedsiębiorstw [zł] oraz $x_3$ - przychody z całkoształtu działalności w badanych przedsiębiorstwach [mln zł]. Zbiór danych obejmuje $P=18$ obserwacji $N=4$ zmiennych. Kolejnym miastom przyporządkowano kolejne numery, a całość przedstawia się następująco:

Nr	Miasto	$x_1$	$x_2$	$x_3$
1	Warszawa	2,4	4430,69	234668,0
2	Białystok	10,0	2866,63	6563,7
3	Bydgoszcz	6,3	2859,86	5390,1
4	Gdańsk	3,6	4176,46	29362,4
5	Gorzów Wlkp.	6,2	2600,14	2863,3
6	Katowice	2,6	4477,81	26787,1
7	Kielce	10,2	2850,63	7077,1
8	Kraków	3,5	3308,41	41180,7
9	Lublin	8,2	2836,65	15021,9
10	Łódź	8,3	2951,00	15223,5
11	Olsztyn	5,6	3040,74	4285,2
12	Opole	5,1	2961014	3015,3
13	Poznań	2,4	3644,28	36011,3
14	Rzeszów	6,6	3149,87	6331,6
15	Szczecin	6,4	3439,94	6700,7
16	Toruń	7,3	3033,04	8228,8
17	Wrocław	4,2	3335,27	24095,7
18	Zielona Góra	6,3	2925,89	2302,1

Z racji tego iż badane zmienne mają różny rząd wielkości, najpierw trzeba je znormalizować. Normalizacji dokonano zgodnie z zależnością: $$ \mb{X}_{norm}=\frac{\mb{X} - \mb{X}_{mean}}{\sigma_\mb{X}}. $$ Po przeprowadzeniu transformacji PCA można pokusić się o przedstawienie zależności dwóch głównych składowych na płaszczyźnie PCA. W wyniku tego uzyskano:

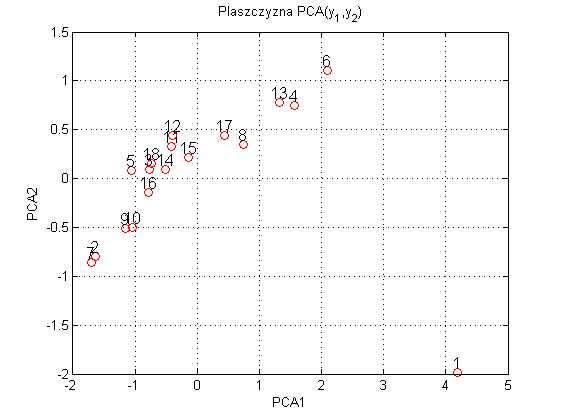
Jaki jest cel takiego postępowania? Otóż uwzględnienie dwóch dominujących składowych z większego zestawu danych umożliwia wyciągnięcie najistotniejszych informacji. W tym przypadku, wiedząc, że pierwotny zestaw danych opisuje wskaźniki dotyczące rozwoju gospodarczego, można bez problemów wywnioskować, że miasta 1, 6, 13, 4 znacząco odstają od reszty. Warto również zauważyć, że pomijając miasto 1, większość miast ułożona jest niemalże liniowo co pozwala wnioskować, że dwie dominujące składowe, są ze sobą w jakiś sposób powiązane.

Do wygenerowania powyższego wykresu użyto poniższego skryptu:

Plik: pca_sample4.m

clear all;
clc;

data = load('data.mat');
X = data.X;

P = size(X,1);

% normalizacja danych
X = (X - repmat (mean(X), P, 1)) ./ repmat (std(X), P, 1);

X = X';

[Y, W, R, R_hat, X_hat] = pca_transform(X, 2);

figure;
y1 = Y(1,:);
y2 = Y(2,:);
for i = 1:numel(y1)
    plot (y1(i), y2(i), 'rO');
    text (y1(i), y2(i), num2str (i),'HorizontalAlignment','center', 'VerticalAlignment', 'bottom', 'FontSize', 12)
    hold on;
end
xlabel ('PCA1');
ylabel ('PCA2');
title ('Plaszczyzna PCA(y_1,y_2)');
grid on;

zaś dane do przykładu dostępne są tutaj: pca_data.mat.

Literatura.

Do niniejszego opracowania wykorzystałem informacje zawarte w książce "Sieci neuronowe do przetwarzania informacji" autorstwa prof. dr hab. inż. Stanisława Osowskiego. Książka dostępna jest między innymi tutaj: Oficyna wydawnicza Politechniki Warszawskiej.