Regulator PID
Mały spis treści:
- Wstęp
- Pętla regulacji
- Struktura regulatora PID
- Strojenie regulatora PID
- Gain scheduling
- Implementacja regulatora - usprawnienia praktyczne
- Regulator dyskretny
Wstęp
Algorytm PID jest chyba najczęściej spotykanym sposobem regulacji wszelkiej maści procesów, zarówno tych mniejszych jak i większych. Swoją popularność zawdzięcza przede wszystkim prostocie, mnogością dostępnych opracowań i badań oraz wszechstronnością. Faktem jest, że nie zawsze regulator PID jest rozwiązaniem optymalnym ale z uwagi na swoją wszechstronność, potrafi lepiej lub gorzej realizować zadania regulacji. Na mojej stronie jest już dostępne nieco informacji na temat PID (PID STM32, Symulator PID) ale postanowiłem zebrać wszystko w jednym miejscu dokładając proste przykłady gdzie i jak używać PIDa, jak stroić i na co zwracać uwagę. Mam nadzieję, że informacje przedstawione tutaj przydadzą się początkującym w uruchomieniu ich pierwszego układu regulacji. Opracowanie przeznaczone jest raczej dla osób rozpoczynających swoją przygodę z układami regulacji.
Pętla regulacji
Omawianie regulacji PID zacząć należy od dokładnego określenia czym jest pętla regulacji, czemu służy oraz gdzie PID znajduje w niej swoje miejsce. Weźmy za przykład prostą wiertarkę, która nie posiada regulacji prędkości obrotowej, możliwa jest tylko regulacja podawanego na silnik napięcia. Użytkownik zadając określone napięcie sterujące silnikiem, może wpływać bezpośrednio na jego prędkość. Co się jednak stanie, jeśli do głowicy wiertarki zostanie przyłożony jakiś moment obciążenia (na przykład użytkownik ręką spróbuje zatrzymać obracającą się głowicę albo przyłoży wiertło do ściany dokładając w ten sposób obciążenie lub na wskutek zużycia części mechanicznych powstanie dodatkowy opór)? Jak nietrudno sie domyślić, prędkość obrotowa silnika spadnie. Użytkownik musi wtedy "na oko" docisnąć przycisk mocy wiertarki aby rozkręcić silnik mocniej i uzyskać pożądane obroty wiertarki.
W przypadku takiego scenariusza mamy do czynienia z przykładem sterowania w pętli otwartej, której ideę przedstawia poniższy rysunek:
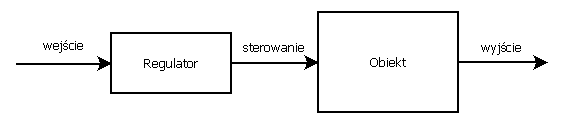
W kontekście omawianego przykładu, wejściem jest zadana moc wiertarki (np. zakres od 0-100%), sterowaniem jest napięcie zasilające silnik, zaś wyjściem jest jego prędkość obrotowa. Zadaniem regulatora w tym problemie jest przetwarzanie wejścia w wielkość sterującą. Takie podejście ma w zasadzie tylko jedną zaletę: jest proste. Największą zaś wadą jest z kolei kompletny brak automatyzacji i wszystkich korzyści jakie z tego wynikają.
Rozpatrzmy drugi przypadek. Użytkownik ma do dyspozycji lepszy model wiertarki, który umożliwia regulację prędkości obrotowej. W jaki sposób jest to zrealizowane? Właśnie z użyciem zamkniętej pętli sterowania czyli pętli ze sprzężeniem zwrotnym. Układ taki obejmuje już implementację bardziej poważnego regulatora, przed którym stawiane są konkretne cele do zrealizowania. Jednym z nich może być przenoszenie na wyjście wielkości wejściowej.
Schemat blokowy podstawowej pętli regulacji pokazano na rysunku poniżej:
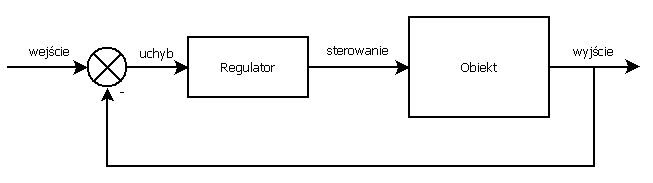
Warto tutaj zwrócić uwagę na kilka kwestii. Pierwszą z nich jest to, że dla przykładu z wiertarką, zmienia się wielkość wejściowa (oznaczana często jako SP - set point, wartość zadana), którą jest teraz zadana prędkość obrotowa. Ta z kolei pomniejszana jest o pomiar aktualnej prędkości kątowej głowicy (MV - measured variable, zmienna mierzona) co skutkuje uzyskaniem nowej wielkości jaką jest uchyb. Uchyb będący różnicą pomiędzy wartością zadaną, a mierzoną jest z kolei wejściem regulatora, który na jej podstawie wyznacza sterowanie obiektu. Uchyb w tym wypadku będzie również wyrażony w jednostkach prędkości obrotowej. Sterowanie oddziałujące na obiekt wywołuje zmianę stanu obiektu, co oczywiście wpływa na wartość wyjścia, które z kolei jest zawracane sprzężeniem zwrotnym (w tym przypadku ujemnym) na wejście całego toru sterowania. Koło się zamyka.
Jakie są zalety takiego rozwiązania? Otóż w zależności od tego co chcemy osiągnąć, można zaimplementować taki algorytm sterowania by np: zerować wartość uchybu w stanie ustalonym (stan ustalony - wszystkie prędkości układu są równe 0; zerowy uchyb oznacza, że wyjście jest równe wartości wejściowej), niwelować wpływ zakłóceń na wyjście (dla przykładu wiertatki będzie to np. hamowanie głowicy w trakcie wiercenia) czy stabilizować układ, który sam w sobie jest niestabilny.
Osobną kwestią jest to, że jeśli chcemy stworzyć pętlę regulacji konieczne jest zastosowanie czujników mierzących wszystkie regulowane wielkości. To z kolei dokłada kolejne człony dynamiczne do całego toru sterowania, które należy następnie uwzględnić w samym algorytmie regulatora. Przemilczałem również fakt, że zazwyczaj wartość sterowania przekazywana jest na obiekt za pośrednictwem urządzenia wykonawczego, które również ma swoją dynamikę. W teorii doprowadza się do sytuacji takiej, gdzie dynamika obiektu jest wynikiem zagregowania dynamiki urządzeń wykonawczych oraz samego obiektu regulacji.
Struktura regulatora PID
Zanim przejdę do omówienia podstawowej i najczęściej spotykanej struktury regulatora PID, warto omówić dokładniej każdy z jego członów. Jak sama nazwa wskazuje, PID składa się z 3 członów:
- P - człon proporcjonalny - reaguje on na bieżące wartości uchybu; parametrem określającym siłę działania członu P jest jego wzmocnienie: $K_p$. Jeśli stosowany jest w pojedynkę, mamy do czynienia z regulatorem typu P. Nie zapewnia zerowania uchybu w stanie ustalonym. Równanie czasowe regulatora typu P dane jest: $$ U_P(t)=K_p e(t), $$ zaś w postaci transmitancyjnej: $$ U_P(s)=K_p. $$
- I - człon całkujący - kumuluje on przeszłe wartości uchybu przechowując w ten sposób informacje o historii działania układu; wpływ członu całkującego na sterowanie regulowane jest czasem całkowania $T_i$. Umożliwia uzyskanie zerowego uchybu regulacji w stanie ustalonym. Pogarsza własności dynamiczne układu. Równanie członu całkującego dane jest jako: $$ U_I(t)=\frac{1}{T_i}\int\limits_{0}^{\tau}{e(t)dt}, $$ gdzie: $\tau$ - horyzont sterowania, $e(t)$ - uchyb regulacji. W postaci transmitacyjnej przedstawia się zaś jako: $$ U_I(s)=\frac{1}{T_i s}. $$
- D - człon różniczkujący - reaguje na przyszłe wartości uchybu; parametrem decydującym o sile działania różniczkowania jest stała różniczkowania $T_d$. Poprawia własności dynamiczne układu choć może powodować wzmocnienie zakłóceń. Równanie czasowe członu D dane jest jako: $$ U_D(t)=T_d \frac{de(t)}{dt}, $$ a w postaci transmitancyjnej: $$ U_D(s)=T_d s $$
Prócz regulatorów PID spotyka się również nieco zubożone regulatory jak np. wcześniej wspomniany regulator typu P. Możliwe jest również wyłączenie członu różniczkującego (regulator PI) w sytuacji, kiedy człon D wpływa negatywnie na uzyskiwane rezultaty. W niektórych przypadkach można zrezygnować z członu całkującego (regulator PD) jeśli celem regulacji nie jest zerowanie uchybu lub jeśli układ sam w sobie ma charakter całkujący (obiekty astatyczne, dla których równanie charakterystyczne układu zamkniętego ma conajmniej jeden pierwiastek o zerowej części rzeczywistej). Aby z regulatora PID uzyskać regulator typu P, należy przyjąć parametry: $$ T_i = \infty, T_d = 0, $$ co bywa pomocne w przypadku przeprowadzania eksperymentu przekaźnikowego o czym mowa w części dotyczącej strojenia PID.
Najpowszechniej stosowaną strukturą regulatora PID jest jego postać równoległa. W przypadku zastosowania wersji zależnej (parametry członów I oraz D są zależne od wzmocnienia członu P) całość prezentuje się następująco:
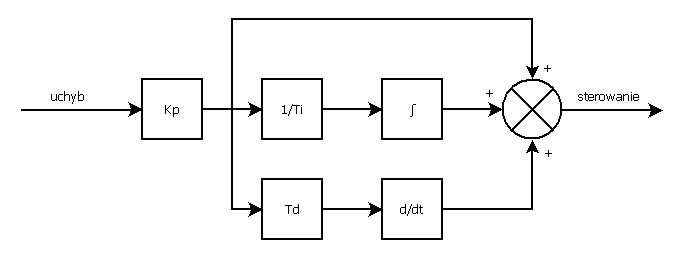
Równanie czasowe takiego regulatora dane jest w postaci: $$ U(t)_{PID}=K_p \left( e(t) + \frac{1}{T_i}\int\limits_{0}^{\tau}{e(t)dt} + T_d \frac{de(t)}{dt} \right), $$ zaś w postaci transmitancji: $$ K_{PID}=K_p \left(1 + \frac{1}{T_i s} + T_d s \right), $$
Alternatywną wersją tej struktury jest postać niezależna, wtedy parametry poszczególnych członów są od siebie odseparowane i mogą być bezpośrednio przeliczane tak jak przedstawiono poniżej:
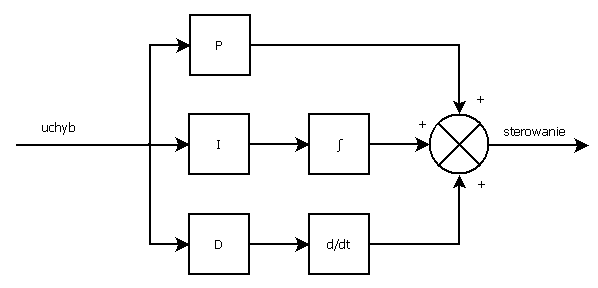
Istotną kwestią, która nieraz przypominana mi była w trakcie studiów jest odpowiedź skokowa regulatora PID. Należy tutaj zwrócić uwagę, że przedstawione powyżej równanie regulatora dotyczy jego idealnej postaci - takiej w której istnieje "czysty" człon różniczkowania. W praktyce takiego rozwiązania nie da się zaimplementować stąd przytoczyć należy równanie regulatora w postaci rzeczywistej: $$ K_{PID}=K_p \left(1 + \frac{1}{T_i s} + \frac{T_d s}{1+\frac{T_d}{\alpha} s} \right), $$
Jak widać człon różniczkujący uzupełniony jest o inercję pierwszego rzędu o odpowiednio dobranym parametrze $\alpha$. Człon inercyjny pełni tutaj rolę filtra dolnoprzepustowego, który uzupełnia transmitancję o dodatkowy biegun. Aby przedstawić odpowiedzi skokowe regulatora PID idealnego oraz rzeczywistego, będę posiłkował się świetnym rysunkiem wziętym ze strony: http://virtual.cvut.cz/course/syscontrol/node61.html, który wyjaśnia więcej niż 1000 słów:
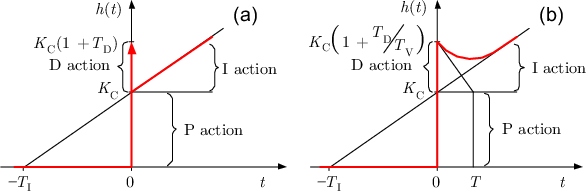
Pora wreszcie na przykłady zastosowania regulacji PID w praktyce. Dany jest układ dynamiczny w postaci funkcji przejścia: $$ K(s) = \frac{2}{(1+2s)(1+3s)}, $$ który objęto ujemnym jednostkowym sprzężeniem zwrotnym. Jako źródło wartości zadanej użyto skoku jednostkowego. Do układu regulacji zastosowano regulator PID o parametrach: $$ K_p=2.0, T_i=5.4, T_d=0.4. $$ Implementacja układu regulacji w środowisku Simulink została przedstawiona poniżej:
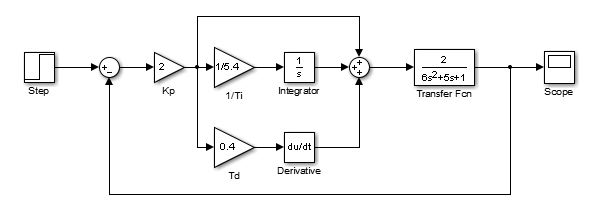
W wyniku symulacji tego układu uzyskano przebieg sygnału wyjściowego:
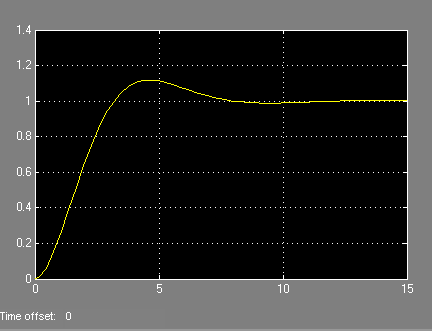
Podobny efekt można uzyskać z użyciem Control System Toolbox w Matlabie przy pomocy poniższego skrypciku:
Plik: pid_1.m
s = tf('s');
plant = 2 / ((1 + 2 * s) * (1 + 3 * s));
Kp = 2.0;
Ti = 5.4;
Td = 0.4;
reg = Kp * (1 + 1/(Ti * s) + Td * s);
closed_loop = (reg * plant) / (1 + reg * plant);
step (closed_loop);
grid on;W wyniku działania powyższego skryptu uzyskano następujący wynik:
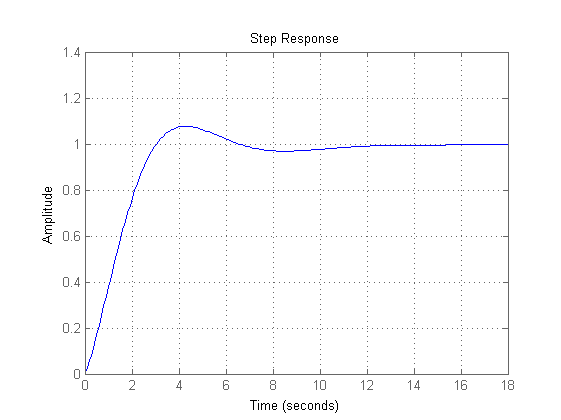
Strojenie regulatora PID
Jak nietrudno się domyślić, regulator sam w sobie niewiele zdziała. Konieczne jest określenie jego parametrów aby możliwe było uzyskanie określonego rezultatu. Tutaj z pomocą przychodzi kilka metod strojenia regulatorów PID, z czego ja postaram się opisać 3 najczęściej spotykane.
Zanim jednak przejdę do omówienia metod strojenia regulatorów chciałem zwrócić uwagę na jeszcze jedną kwestię, która może okazać się pomocna początkującym. Wszystkie przykłady w tym opracowaniu są bezwymiarowe i oderwane nieco od rzeczywistości. W praktyce układ regulacji zajmuje się sterowaniem rzeczywistych obiektów stąd wszystkie informacje w układzie zazwyczaj mają swój wymiar. Dla przytoczonego wcześniej schematu najprostszej pętli regulacji (regulator, obiekt i sprzężenie zwrotne) warto pokusić się o chwilę refleksji nad tym w jakiej jednostce wyrażone będą nastawy regulatora. Dla przykładu sterowania prędkością kątową wiertarki (sterowanie napięciem na silniku $U[V]$, pomiar prędkości kątowej $\omega [\frac{rad}{s}]$), zakładając obecność regulatora proporcjonalnego oraz zgodnie z zależnością: $$ U_{reg}(t)=K_p e(t), $$ gdzie: $U_{reg}(t)$ - wyjście regulatora, $e(t)$ - uchyb regulacji, łatwo wyliczyć, że wzmocnienie musi być wyrażone jako: $$ \frac{U [V]}{\omega [\frac{rad}{s}]}=\frac{Vs}{rad}. $$
Strojenie regulatora PI dla obiektu pierwszego rzędu
Na pierwszy ogień idzie metoda stosowania w przypadku szczególnym, rzadko spotykanym w praktyce: strojenie regulatora dla obiektu pierwszego rzędu. Przykład ten jest ciekawy chociażby z tego względu, że jeśli celem układu regulacji ma być zerowanie uchybu, teoretycznie wystarczyłby regulator typu P. Skąd to wiadomo? Zacząć należy od ogólnego schematu pętli regulacji tak jak na rysunku:
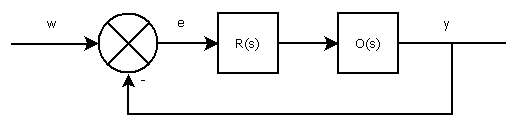
gdzie: $w(t)$ - sygnał wejściowy, $y(t)$ - sygnał wyjściowy, $e(t)$ - uchyb, $R(s)$ - transmitancja regulatora, $O(s)$ - transmitancja obiektu. Transmitancja całego układu (stosunek transformaty wyjścia do transformaty wejścia) dana jest w postaci: $$ K(s)=\frac{Y(s)}{W(s)}=\frac {R(s)O(s)}{1+R(s)O(s)}. $$ Jeśli zaś interesowałaby nas transmitancja będąca stosunkiem uchybu do wejścia, transmitancja przyjmie postać: $$ K_e(s)=\frac{E(s)}{W(s)}=\frac {1}{1+R(s)O(s)}, $$ gdzie: $E(s)$ - transformata uchybu. Przy założeniu stabilności układu (to bardzo istotne założenie!), można wyznaczyć wartość uchybu w stanie ustalonym z zależności: $$ e_{ust}=\lim_{t\to\infty} {e(t)}=\lim_{s\to 0} {sE(s)}. $$ Do wyznaczenia wielkości $E(s)$ można wykorzystać wcześniejsze równanie uzyskując: $$ E(s)=W(s)K_e(s). $$ Podstawiając do siebie odpowiednie równania uzyskać można: $$ e_{ust}=\lim_{s\to 0} {sW(s)\frac {1}{1+R(s)O(s)}}. $$ Uwzględniając, że wejście jest skokiem jednostkowym, zastosowanym regulatorem jest regulator typu P zaś sterowanym obiektem jest inercja I rzędu: $$ w(t)=\mb{1}(t), \quad W(s)=\frac{1}{s}, \quad R(s)=K_p, \quad O(s)=\frac{k}{1+sT}, $$ otrzymuje się ostatecznie zależność: $$ e_{ust}=\lim_{s\to 0} {s \frac{1}{s} \frac {1}{1+K_p\frac{k}{1+sT}}}, $$ i po kilku przekształceniach: $$ e_{ust}=\lim_{s\to 0} \frac{1+sT}{1+sT+K_p k}= \frac{1}{1+K_p k}. $$ Na podstawie powyższej zależności można zauważyć, że wraz ze wzrostem $K_p$, wartość uchybu w stanie ustalonym maleje. Stąd: $$ K_p=\infty, e_{ust} \rightarrow 0. $$ W praktyce to rozwiązanie jest nierealizowalne. Dodatkowo wysokie wzmocnienie może zwiększyć wrażliwość całego układu sterowania na zakłócenia. Wracając do strojenia regulatora dla układu I rzędu. Jedną z metod, na którą miałem okazję się natknąć jest przyjęcie stałej całkowania regulatora PI takiego jak stała czasowa układu, zaś wzmocnienie regulatora dobierane jest doświadczalnie zgodnie z zasadą (dla przyjętych wcześniej oznaczeń parametrów modelu i regulatora): $$ T_i=T, K_p=\frac {T}{\alpha k}, $$ gdzie: $\alpha$ dobierana jest z zakresu: $$ \alpha=<0.1..1>T. $$ Aby zobrazować działanie tej metody przygotowałem prosty model układu regulacji dla obiektu będącego inercją I rzędu w Simulinku: PID_model1.slx oraz skrypt uruchamiający symulacje:
Plik: pid_script1.m
sim_t = 10;
k = 2;
T = 3;
Kp = 2;
Ti = 0.5;
figure;
color_ptr = 0;
x = 0.1:0.1:1;
plots = numel(x);
for i = 0.1:0.1:1
Ti = T;
Kp = T / (i * T * k);
sim ('pid_model1.slx');
plot (tout, y, 'Color', [1 - color_ptr * 1 / plots, 0, 0]);
hold on;
color_ptr = color_ptr + 1;
end
sim ('model1.slx');
plot (tout, y);Po uruchomieniu skryptu uzyskano wyniki takie jak przedstawiono poniżej. Kolorem czerwonym zaznaczona jest odpowiedź układu na skok jednostkowy dla najbardziej agresywnej nastawy $K_p=\frac{T}{0.1Tk}$, zaś na niebiesko dla najłagodniejszej.
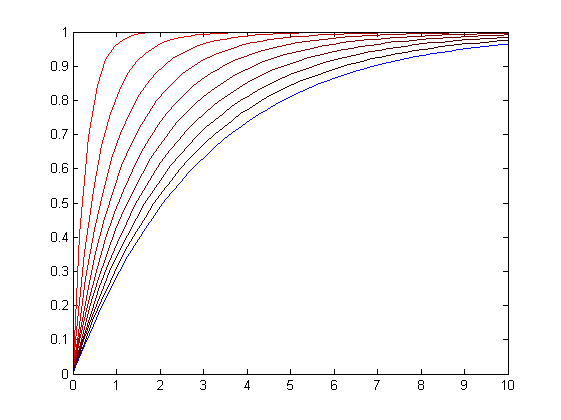
Metoda Zieglera-Nicholsa - analiza odpowiedzi skokowej
Metodą strojenia, której ja jestem zwolennikiem i którą zdarzało mi się wykorzystywać bardzo często jest analiza odpowiedzi skokowej układu. Główna zasada tej metody opiera się na przybliżeniu odpowiedzi układu na wymuszenie skokowe modelem będącym inercją I rzędu z opóźnieniem. Wymagane jest tutaj nieco więcej przeliczeń niż w przypadku klasycznego eksperymentu Zieglera-Nicholsa. Metoda ta z oczywistych względów nie nadaje się do strojenia obiektów pierwszego rzędu. Jeśli już uda się dopasować model inercyjny do uzyskanego przebiegu, odczytywane są 3 wartości, które z kolei przeliczane są konkretne nastawy regulatora. Wielkości te to $k$ - wzmocnienie układu, $t_1$ - czas po którym układ osiąga 63.2% wartości stanu ustalonego oraz $t_2$ - czas po którym układ uzyskuje 28.3% tego stanu. Inercja I rzędu z opóźnieniem dana jest w postaci transmitancji: $$ K(s)=\frac{k}{1+sT}e^{-sT_0}, $$ gdzie: $k$ - wzmocnienie, $T$ - stała czasowa, $T_0$ - opóźnienie. Aby wyliczyć te wielkości należy posłużyć się wcześniej uzyskanymi parametrami zgodnie z zasadami: $$ k=\frac{\Delta y}{\Delta u},\quad T=1.5(t_1-t_2),\quad T_0=t_1-T, $$ gdzie: $\Delta y$ - przyrost wyjścia obiektu od poprzedniego stanu ustalonego. $\Delta u$ - przyrost sterowania. Mając do dyspozycji parametry zidentyfikowanego modelu można wyznaczyć szereg nastaw w zależności od rozwiązania. Czemu mowa jest o przyrostach wartości wyjścia i sterowania? Ponieważ możliwe jest identyfikowanie zachowania obiektu w zależności od jego punktu pracy. Wprowadza się jeszcze pomocniczą wartość określoną wzorem: $$ a = \frac {kT_0}{T}, $$ zaś nastawy zaproponowane przez Zieglera-Nicholsa podane są w tabeli:
| Typ regulatora | Nastawy |
| P | $K_p=\frac{1}{a}$ |
| PI | $K_p=\frac{0.9}{a} \\ T_i=3T_0$ |
| PID | $K_p=\frac{1.2}{a}\\ T_i=2T_0 \\ T_d=\frac{T_0}{2}$ |
Pora na przykład. Dany jest układ dynamiczny w postaci transmitancji: $$ K(s)=\frac{3}{4s^2 + 4s + 1}, $$ którego odpowiedź na wymuszenie skokowe o wartości 2, wraz z zaznaczonymi chwilami czasu dla którego układ uzyskuje 28.3% oraz 63.2% stanu ustalonego, przedstawia się następująco:
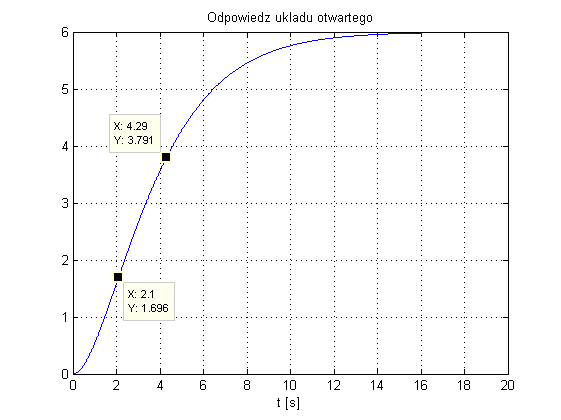
Do stworzenia dopasowania inercją I rzędu z opóźnieniem należy wyznaczyć wzmocnienie obiektu: $k=\frac{6}{2}=3$ oraz odczytać z wykresu niezbędne czasy: $t_1=4.29$, $t_2=2.1$. Parametry inercji dane są jako: $$ k=3, \\T=1.5(4.29 - 2.1)=3.285, \\T0=4.29-3.285=1.005. $$ Dla takich parametrów dopasowanie modelu do odpowiedzi obiektu prezentuje się tak jak pokazano poniżej:
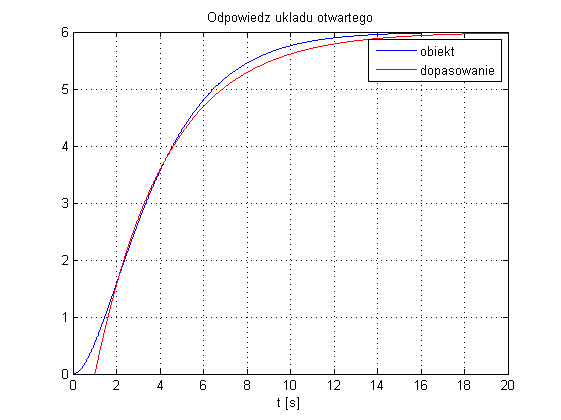
Korzystając z wcześniej przytoczonej tabelki oraz wyznaczając dodatkowy parametr $a=0.9178$ uzyskuje się ostatecznie nastawy regulatora PID: $$ K_p=1.3075, \\ T_i=2.01, \\ T_d=0.5025. $$ Odpowiedź układu zamkniętego z regulatorem PID nastrojonym tymi parametrami przedstawiono poniżej:
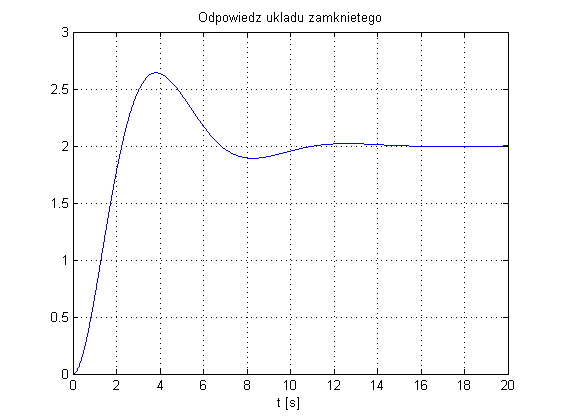
I na koniec udostępniam model z użyciem, którego wygenerowane zostały powyższe wyniki: PID_model3.slx oraz skrypt uruchamiający symulację:
Plik: pid_script3.m
% czas symulacji
tSim = 20;
% parametry obiektu
numO = 3;
denO = [4 4 1];
% parametry dopasowania
k = 3;
T = 3.285;
T0 = 1.005;
% parametry regulatora
Kp = 1.3075;
Ti = 2.01;
Td = 0.5025;
sim('pid_model3.slx');
figure;
plot (tout, open, 'b'); hold on;
plot (tout, model, 'r');
title ('Odpowiedz ukladu otwartego');
xlabel('t [s]'); grid on;
legend ('obiekt', 'dopasowanie');
figure;
plot (tout, closed);
title ('Odpowiedz ukladu zamknietego');
xlabel('t [s]'); grid on;Metoda Chiena-Hrones-Reswicka - analiza odpowiedzi skokowej
Pewnym urozmaiceniem powyższej metody strojenia jest metoda CHR, która również bazuje na analizie odpowiedzi skokowej układu. Autorzy tej metody zaproponowali dodatkowo sposób doboru regulatora w zależności od parametru $R$, który dany jest jako: $$ R=\frac{T}{T0}. $$ Propozycje użycia regulatorów pokazano w tabeli poniżej:
| Typ regulatora | $R$ |
| P | $R>10$ |
| PI | $7.5<R<10$ |
| PID | $3<R<7.5$ |
| wyższy rząd | $R<3$ |
Dla wcześniej przytoczonego przykładu uzyskuje się: $$ R=3.2687, $$ zatem ta wartość idealnie wpisuje się w zakres przeznaczony regulatorowi PID. Autorzy proponują dwa komplety nastaw w zależności od nadrzędnego celu regulacji: odpowiedź aperiodyczna (bez przeregulowań) oraz 20% przeregulowanie. Mając wyznaczone wielkości takie jak $a$, $T$ oraz $T0$, nastawy dla poszczególnych regulatorów przedstawiają się następująco:
| Odpowiedź aperiodyczna | |
| Typ regulatora | Nastawy |
| P | $K_p=\frac{0.3}{a}$ |
| PI | $K_p=\frac{0.35}{a} \\ T_i=1.2T$ |
| PID | $K_p=\frac{0.6}{a}\\ T_i=T \\ T_d=0.5T_0$ |
| Przeregulowanie 20% | |
| Typ regulatora | Nastawy |
| P | $K_p=\frac{0.7}{a}$ |
| PI | $K_p=\frac{0.6}{a} \\ T_i=T$ |
| PID | $K_p=\frac{0.95}{a}\\ T_i=1.4T \\ T_d=0.47T_0$ |
Metoda Zieglera-Nicholsa - analiza drgań granicznych
Jedną z najczęściej spotykanych metod strojenia jest analiza drgań graniczych układu zamkniętego. Metoda ta sprowadza się do wyznaczenia granicznego wzmocnienia regulatora proporcjonalnego, dla którego układ zamknięty wchodzi w stan niegasnących oscylacji. Istotna jest również informacja o okresie tych drgań. Te dwie wielkości (wzmocnienie graniczne oraz okres drgań) służą z kolei do wyznaczenia wartości nastaw regulatorów.
Najprościej jest posłużyć się przykładem. Obiekt sterowania dany jest w postaci transmitancji: $$ K(s)=\frac{3}{2s^3+5s^2+2s+1}. $$ Odpowiedź skokowa takiego układu prezentuje się następująco:
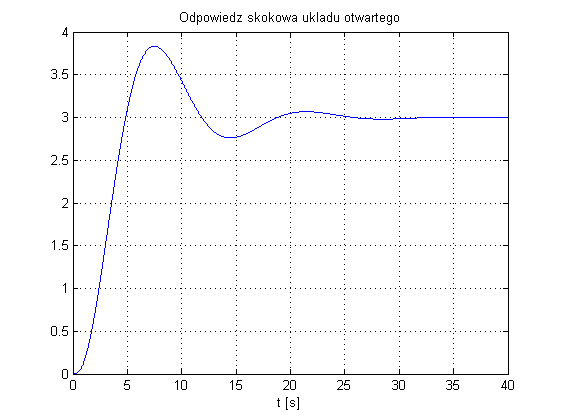
zaś graniczne wzmocnienie, dla którego układ zamknięty utrzymuje się w stanie niegasnących oscylacji ustalono na: $K_{gr}=1.33$:
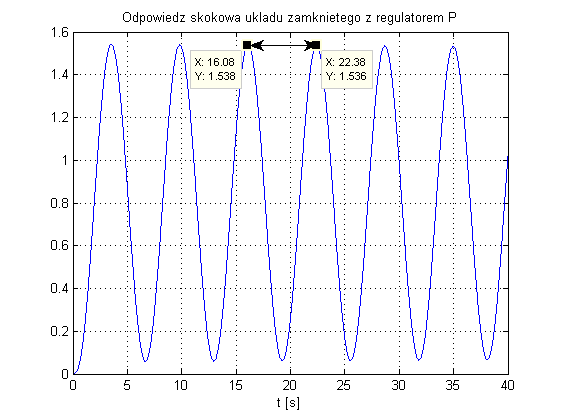
Jak można odczytać z wykresu, okres drgań wynosi w przybliżeniu: $T_{gr}=6.3$. Mając do dyspozycji wartość granicznego wzmocnienia oraz okres oscylacji można wyznaczyć parametry regulatorów zgodnie z tabelką:
| Typ regulatora | Nastawy |
| P | $K_p=0.5K_{gr}$ |
| PI | $K_p=0.45K_{gr} \\ T_i=0.85T_{gr}$ |
| PID | $K_p=0.6K_{gr} \\ T_i=0.5T_{gr} \\ T_d=0.12T_{gr}$ |
Zgodnie z powyższym uzyskuje się nastawy: $$ K_p=0.80, \\ T_i=3.15, \\ T_d=0.76, $$ dla których przebieg wyjścia układu regulacji przedstawia się następująco:
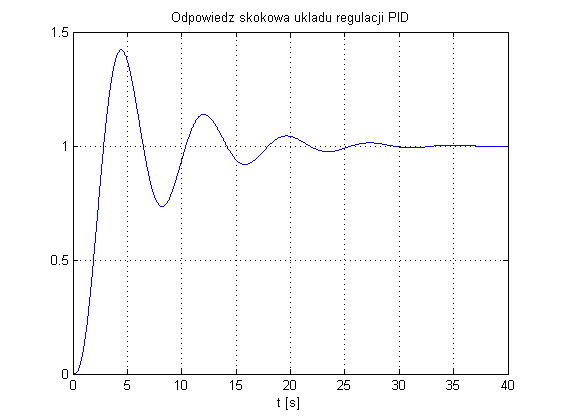
Jak nietrudno zauważyć, odpowiedź układu może nie być satysfakcjonująca dlatego w tym przypadku metoda Zieglera-Nicholsa powinna posłużyć jako punkt startowych szukania nastaw. Po dokręceniu nastaw w PID Tunerze uzyskano parametry regulatora PID: $$ K_p=0.45, \\ T_i=4.03, \\ T_d=1.01, $$ dla których uzyskano przebieg:
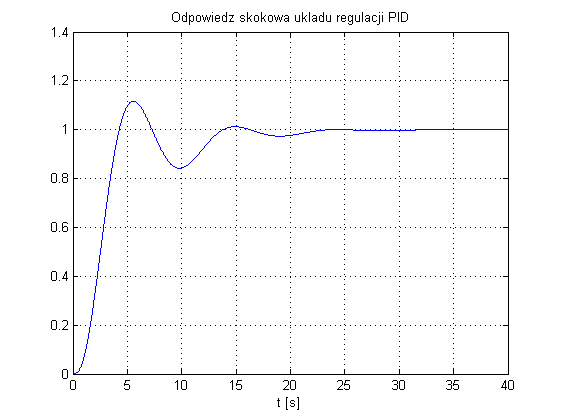
Na zakończenie, chciałem dodać, że metodę tę stosuje się w tzn. eksperymencie przekaźnikowym. Jeśli mamy do czynienia z działającym już układem regulacji w oparciu o regulator PID, tenże regulator można przekształcić w regulator typu P zgodnie ze wskazówkami opisanymi wcześniej. Dla odpowiednio dużej wartości wzmocnienia regulatora P, uzyskuje się działanie podobne do sterowania przekaźnikowego.
Do wygenerowania powyższych wyników użyty został model: PID_model2.slx oraz poniższy skrypt:
Plik: pid_script2.m
% czas symulacji
tSim = 40;
% licznik transmitancji obiektu
numO = 3;
% mianownik transmitancji obiektu
denO = [2 5 2 1];
% graniczne wzmocnienie do Z-N
Kgr = 1.33;
% nastrojony wg Z-N PID
Kp = 0.8;
Ti = 3.15;
Td = 0.76;
sim ('pid_model2.slx');
figure;
plot (tout, open);
title ('Odpowiedz skokowa ukladu otwartego');
xlabel ('t [s]'); grid on;
figure;
plot (tout, tune);
title ('Odpowiedz skokowa ukladu zamknietego z regulatorem P');
xlabel ('t [s]'); grid on;
figure;
plot (tout, closed);
title ('Odpowiedz skokowa ukladu regulacji PID');
xlabel ('t [s]'); grid on;Strojenie ręczne
Jak można zauważyć na powyższych przykładach, przytoczone metody strojenia stanowią tylko bazę wypadową do określenia startowej wartości parametrów regulatora PID. Każda z nich obarczona jest pewną niedokładnością i ostatecznie (przy braku dostępu do bardziej wyrafinowanych metod strojenia) osoba projektująca układ regulacji zmuszona jest do ręcznego dostrojenia nastaw.
Wadą tej metody jest oczywiście to, że wymaga pewnej wprawy oraz obejmuje szereg eksperymentów stąd konieczna jest dostępność dosyć dokładnego modelu, no chyba, że ktoś ma możliwość eksperymentowania na samym obiekcie regulacji. Nie ma też żadnej uniwersalnej metody strojenia ręcznego ponieważ każdy obiekt może przejawiać zupełnie inną dynamikę. Warto jednak przytoczyć małą tabelkę, która pokazuje, czego się można spodziewać wraz ze zmianą poszczególnych nastaw regulatora PID:
| Parametr | Stabilność | Przeregulowanie | Czas regulacji |
| zwiększenie $K_p$ | pogorszenie | zwiększenie | niewielka zmiana |
| zwiększenie $T_i$ | poprawa | zmniejszenie | zmniejszenie |
| zwiększenie $T_d$ | poprawa | zmniejszenie | niewielkie zmniejszenie |
Najlepszym rozwiązaniem jest rozpoczęcie strojenia od przyjęcia niskiej wartości wzmocnienia proporcjonalnego oraz wyłączenie całkowania i różniczkowania ($T_i=\infty$, $T_d=0$). Z powodu braku członu całkującego, w układzie regulacji w stanie nieustalonym powinien być obecny niezerowy uchyb (możliwe, że będzie zerowy, co wyjaśniono wyżej). Następnie należy zwiększać $K_p$ do czasu aż w układzie pojawią się oscylacje. Wtedy dobrze jest ustawić czas całkowania równy okresowi oscylacji: $T_i=t_{osc}$. Parametr $T_i$ można też dopasować tak, aby zerowanie uchybu przebiegało w zadowalającym tempie jednak należy mieć na uwadze to, że człon całkujący pogarsza własności dynamiczne. Ostatnim krokiek jest stopniowe zwiększanie wartości nastawy $T_d$ tak aby uzyskać zadowalające tłumienie oscylacji w uzyskanych przebiegach.
Osobną sprawą jest zastosowanie bardziej wyszukanych algorytmów strojenia jednak ten temat znacząco wykracza poza zakres tego podstawowego opracowania. W trakcie przygotowywania przykładów na potrzeby tego artykułu posiłkowałem się PID Tunerem, jednego z toolboxów Matlaba.
Gain scheduling
Do tej pory omawiane były przykłady sterowania obiektami dynamicznymi o pewnej szczególnej cesze. Były to obiekty liniowe tzn. takie, których modele dało się przedstawić w formie transmitancji operatorowej lub liniowego równania różniczkowego (lub układu liniowych równań różniczkowych). Układy te mają tę własność, że w ich przypadku możliwe jest stosowanie zasady superpozycji: odpowiedź układu na sumę wymuszeń jest sumą odpowiedzi na każde z tych wymuszeń z osobna. Dodatkowo układy liniowe zapewniają niezmienne wzmocnienie niezależnie od punktu pracy. Oczywistym jest również, że ich charakterystyka statyczna (zależność wyjścia od wejścia dla stanów ustalonych) jest liniowa. Co jednak jeśli zachodzi potrzeba sterowania obiektem, który liniowy nie jest? Tutaj z pomocą przychodzi gain scheduling będący metodą dobory parametrów regulatora w zależności od aktualnego punktu pracy obiektu.
Załóżmy, że obiektem sterowania jest układ, którego model sprowadza się do poniższego równania różniczkowego: $$ \ddot{y}=-\dot{y}-\sqrt{y}+u. $$ Dla stanu ustalonego (wszystkie prędkości w układzie równe 0: $\ddot{y}=0$, $\dot{y} = 0$) otrzymuje się następującą charakterystykę statyczną: $$ y=u^2. $$ Odpowiedź tego układu na serię trzech skoków jednostkowych przedstawiono na rysunku poniżej:
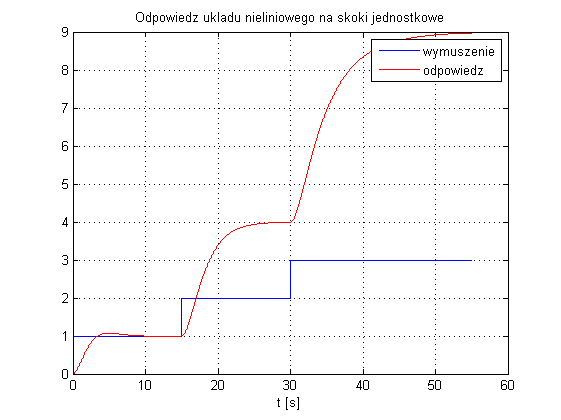
zaś wykorzystany model Simulinka prezentuje się następująco:
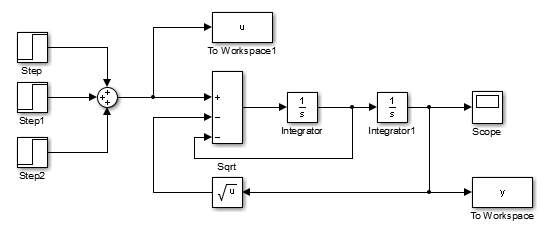
Model i skrypt uruchamiający dostępne są tutaj: pid_model5.slx, pid_script5.m. Jak nietrudno zauważyć, model jest nieliniowy oraz uzyskane wartości stanów ustalonych zgadzają się charakterystyką statyczną. Dla takiego obiektu konieczne jest zastosowanie większej ilości nastaw tak aby układ regulacji spełniał swoje zadanie. Jeśli zastosowany byłby jeden zestaw parametrów regulatora, nastrojony dla pierwszego segmentu, okazałoby się, że dla późniejszych punktów pracy układ byłby niestabilny.
Pierwszym krokiem do uruchomienia gain schedulingu jest wyznaczenie nastaw regulatora PID dla konkretnych punktów pracy. Na wykresie zaznaczone są trzy skoki jednostkowe więc posłużą one do wyznaczenia wszystkich potrzebnych parametrów modeli zastępczych (inercja I rzędu z opóźnieniem) zgodnie ze wcześniej pokazanymi formułami. Po odczytaniu czasów $t_1$ oraz $t_2$ dla każdego z fragmentów przebiegu uzyskano: $$ t_{1,2}=0.99, t_{1,1}=1.87 \\ t_{2,2}=16.77, t_{2,1}=18.61 \\ t_{3,2}=32.48, t_{3,1}=35.49 $$ zaś wyznaczenie wzmocnienia nie powinno stanowić problemów ponieważ zastosowano wymuszenia jednostkowe. Pierwszy indeks dolny oznacza wartość parametru dla danego fragmentu odpowiedzi układu. Ostatecznie parametry modeli inercyjnych przedstawiają się: $$ k_1=1, T_1=1.32, T_{1,0}=0.55 \\ k_2=3, T_2=2.76, T_{2,0}=0.85 \\ k_3=5, T_3=4.515, T_{3,0}=0.975 $$ Jedna mała uwaga. Czasy opóźnień muszą być liczone (tak jak i inne wielkości) względem momentu w którym nastąpiła zmiana wejścia. Ostatecznie dopasowania inercją I rzędu z opóźnieniem przedstawia się jak na rysunku:
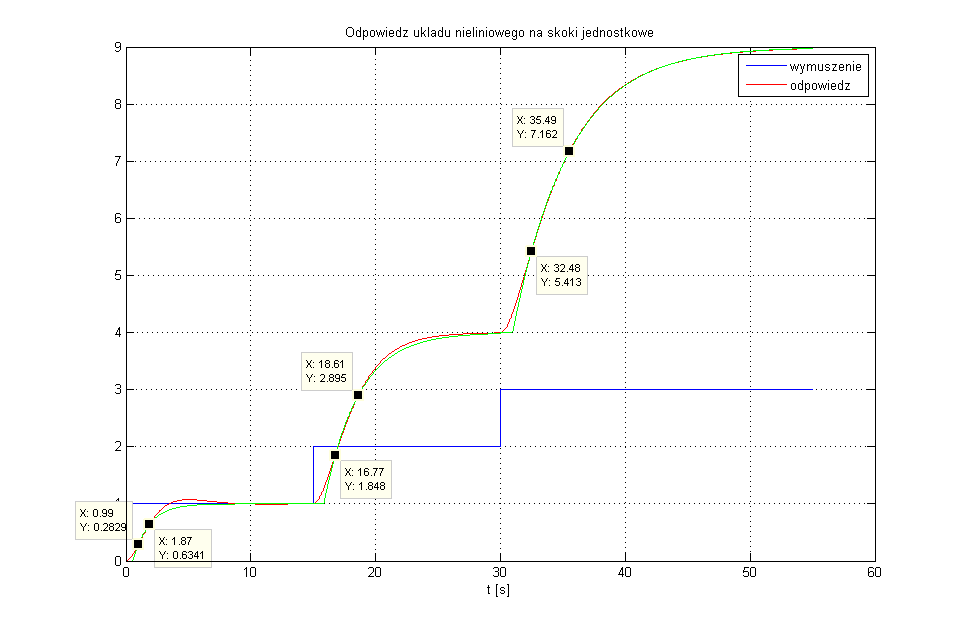
Nastawy regulatora PID wyznaczone zgodnie z formułami Zieglera-Nicholsa wynoszą: $$ K_{p,1} = 2.8800, T_{i,1}=1.1000, T_{d,1}=0.2750 \\ K_{p,2} = 1.2988, T_{i,2}=1.7000, T_{d,2}=0.4250 \\ K_{p,3} = 1.1114, T_{i,3}=1.9500, T_{d,3}=0.4875 $$ Dla tak wyznaczonych nastaw, warto wyznaczyć sobie zależność poszczególnej nastawy od wartości punktu pracy (startowa wartość wyjścia obiektu). Następnie można dokonać aproksymacji danych z użyciem funkcji tak jak przedstawiono poniżej:
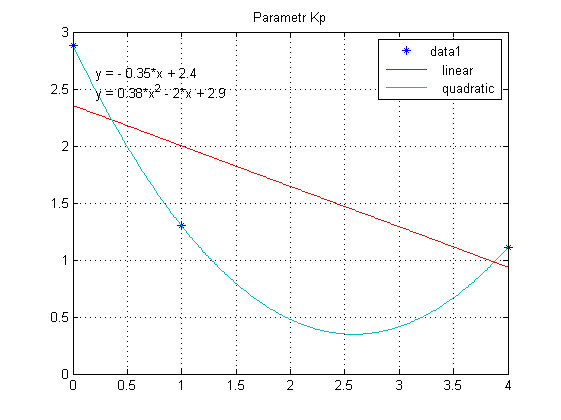
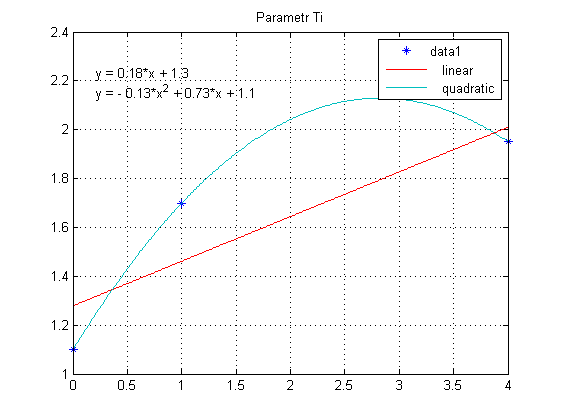
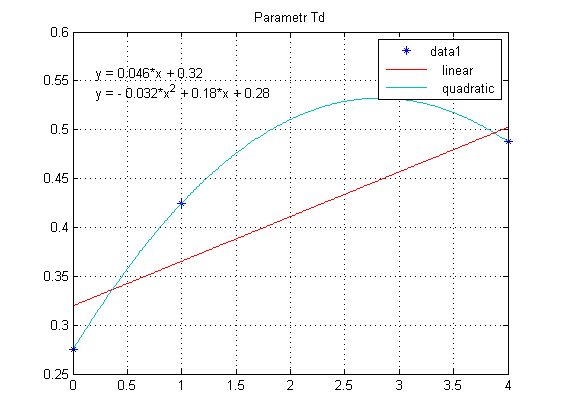
Wiadomo, że charakterystyka statyczna jest funkcją kwadratową stąd do algorytmu sterowania warto wybrać właśnie interpolację parabolą. Nastawy regulatora zamiast wartości stałych, przyjmują postać funkcji zależnej od aktualnego stanu wyjścia obiektu. Regulację PID z funkcyjnie zadanymi nastawami realizuje poniższy model:
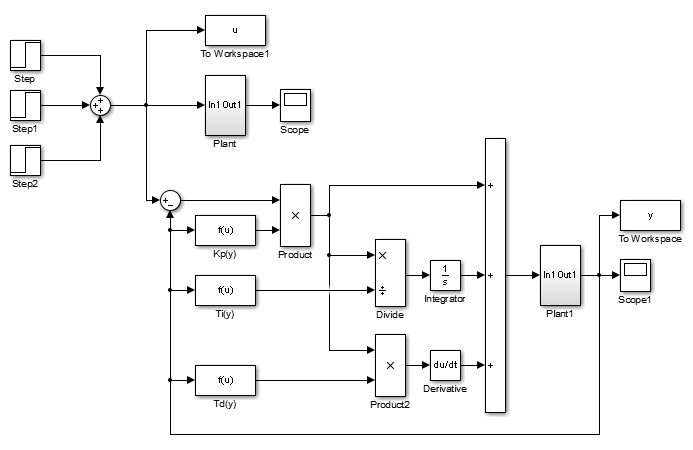
dostępny do pobrania tutaj: pid_model6.slx. W subsystemach zamknięto sam obiekt regulacji. Bloki funkcyjne zawierają z kolei przedstawione wcześniej funkcje interpolacyjne dla każdej z nastaw. W wyniku symulacji uzyskano następujący przebieg wyjścia obiektu:
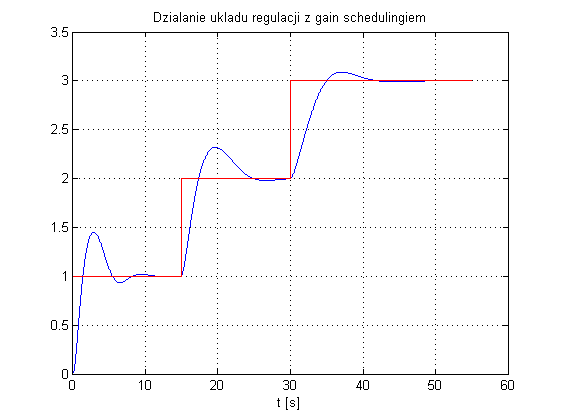
Jak widać, układ działa poprawnie choć dla pierwszego punktu pracy konieczne byłoby lepsze dostrojenie regulatora.
Implementacja regulatora - usprawnienia praktyczne
W praktyce implementacji regulatorów PID stosuje się dodatkowe usprawnienia mające zapewnić prawidłowe działanie układu regulacji. Bez części z nich, algorytm działałby niewłaściwie i nie spełniałbym założonych przez konstruktora celów. Do najważniejszych z nich można zaliczyć:
-
Ograniczenie wielkości sterującej, ograniczenie prędkości wielkości sterującej
Z uwagi na ograniczenia technologiczne wynikające z budowy urządzeń wykonawczych oraz samego obiektu, wprowadza się dodatkowe ograniczenia na wartość sterowania z regulatora. Ma to za zadanie ochronić urządzenia sterujące przed działaniem poza bezpiecznym zakresem lub zbyt gwałtowną zmianą wartości sterującej.
-
Zabezpieczenie przed nasyceniem członu całkującego (mechanizm anti-windup)
Jeśli układ regulacji oprze się na ograniczeniu sterowania, może dojść do sytuacji powstania niezerowego uchybu, który będzie odkładał się na członie całkującym. Z racji niemożliwości doprowadzenia obiektu sterowania do wartości zadanej, powstanie kumulujący się błąd czasowo paraliżujący działanie regulatora. Jeśli człon całkujący ulegnie nasyceniu, a sam układ regulacji zostanie przeprowadzony do innego, możliwego do osiągnięcia punktu zadanego, regulator najpierw będzie musiał pozbyć się (odwinąć) nadmiaru zsumowanego błędu co doprowadzi do niewłaściwego działania układu. Konieczna jest zatem detekcja przekroczenia przez wartość sterującą bezpiecznego zakresu oraz wyłączenie całkowania na czas opierania się układu o ograniczenia sterowania.
-
Bezuderzeniowe przełączanie pracy automatycznej i manualnej
Układy regulacji mają zazwyczaj możliwość przełączania sie pomiędzy pracą automatyczną, a manualną. Nietrudno domyślić sie, że w momencie kiedy układ pracuje w trybie ręcznym, gwałtowne włączenie układu regulacji może spowodować gwałtowne zmiany w działaniu obiektu. Sytuacja ma się podobnie w przypadku wyłączenia pracy automatycznej i przejście w tryb ręczny - może wystąpić niepożądana, skokowa zmiana wartości sterującej. Konieczne jest zatem zadbanie o to, aby pomiędzy tymi trybami układ regulacji przełączał się bezuderzeniowo. Algorytm sterowania musi śledzić wartość sterującą z regulatora tak, aby przełączenie w tryb manualny zachodziło bez problemów. W drugą stronę sprawa jest bardziej skomplikowana ponieważ trzeba wymusić na regulatorze odpowiednią wartość sterowania w momencie przełączenia co wymaga niezbędnych kalkulacji, zgodnie z przyjętym w regulatorze prawem sterowania.
Regulator dyskretny
Nadeszła pora na odrobinę praktyki. W przypadku tworzenia jakiegokolwiek projektu, którego elementem jest układ regulacji, prędzej czy później zachodzi konieczność implementacji cyfrowego regulatora PID. Najczęściej spotykaną formułą cyfrowego PIDa jest: $$ u(i)=K_p\left(e(i)+\frac{h}{T_i}\sum_{k=0}^{i} e(k)+T_d\frac{e(i)-e(i-1)}{h}\right). $$ Jak nietrudno zauważyć, wartość członu całkującego wyznaczana jest całkowaniem numerycznym metodą prostokątów, zaś człon różniczkujący przybliżany jest metodą różnicy wstecznej.
Na potrzeby opracowania przygotowałem krótki kod w C, który realizuje symulację układu sterowania. Wyniki symulacji zapisywane są do plików tekstowych, skąd można je w prosty sposób zwizualizować np. w Matlabie. Kod zawiera niezbędne komentarze więc nie powinno być problemów z zorientowaniem się co jest co. Obiektem regulacji jest układ będący inercją II rzędu w postaci: $$ K(s)=\frac{3}{(1+2s)(1+3s)}, $$ która została przekształcona w układ równań różniczkowych: $$ \begin{cases} \dot{x}_1=x_2 \\ \dot{x}_2=-\frac{T_1+T_2}{T_1T_2}x_2-\frac{1}{T_1T_2}x_1+\frac{k}{T_1T_2}u \end{cases} $$ gdzie: $x_1$ - odpowiedź obiektu, $x_2$ - prędkość odpowiedzi obiektu ($\dot{x}_1$), $T_1, T_2, k$ - parametry inercji II rzędu, $u$ - wartość sygnału na wejściu obiektu. Do całkowania numerycznego równań różniczkowych użyto najprostszej z metod - metodu Eulera. Regulator zrealizowany jest według wcześniej przytoczonej formuły wraz z ograniczeniem wartości wielkości sterującej oraz mechanizmem anti-windup. Regulator został nastrojony z użyciem PID Tunera. Wyniki symulacji układu otwartego oraz układu regulacji przedstawiają się następująco:
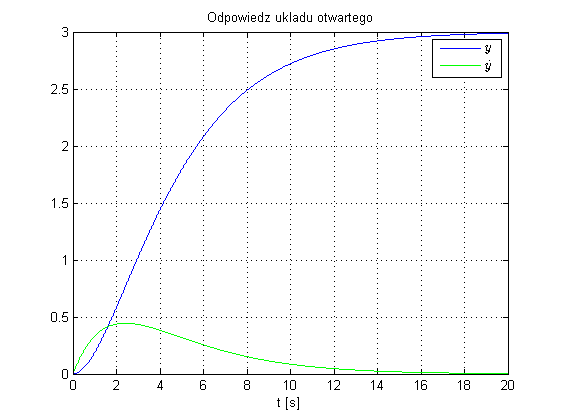
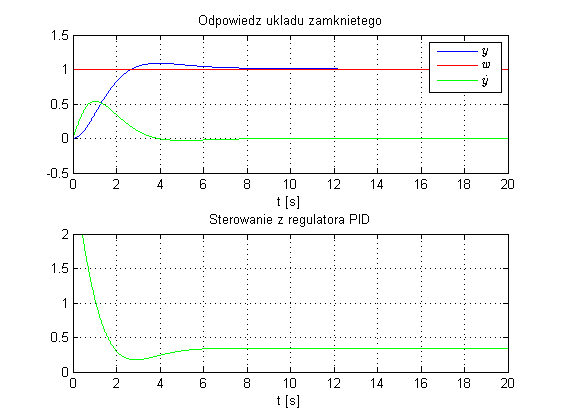
Kod użyty do wygenerowania wyników dostępny jest poniżej:
Plik: pid_test.c
#include
#include
typedef struct st {
float x1;
float x2;
} state;
// rownania rozniczkowe
state inert2_diffs (state current, float u) {
state diffs;
// parametry ukladu dynamicznego
float k = 3.0;
float T1 = 2.0;
float T2 = 3.0;
float mult = T1 * T2;
diffs.x1 = current.x2;
diffs.x2 = -(T1 + T2) / mult * current.x2 - 1 / mult * current.x1 + k / mult * u;
return diffs;
}
// calkowanie rownan rozniczkowych z uzyciem metody Eulera
state euler_inert2 (state previous, float u, float h) {
state next;
state diffs = inert2_diffs (previous, u);
next.x1 = previous.x1 + h * diffs.x1;
next.x2 = previous.x2 + h * diffs.x2;
return next;
};
// symulacja ukladu otwartego
void open_loop (float t_sim, float h, float u) {
FILE *f = fopen("open.txt", "w");
float t = 0.0;
state s;
// warunek poczatkowy
s.x1 = 0.0;
s.x2 = 0.0;
while (t <= t_sim) {
fprintf(f, "%.4f;%.4f;%.4f\n", t, s.x1, s.x2);
s = euler_inert2 (s, u, h);
t += h;
}
fclose (f);
}
// implementacja cyfrowego regulatora PID
float pid (float e, float h) {
float val = 0.0;
// nastawy regulatora
float Kp = 2.9635;
float Ti = 4.8004;
float Td = 0.7152;
// wartosc maksymalna i minimalna sterowania
float max_u = 2.0;
float min_u = -2.0;
// wartosci sterowania z poszczegolnych czlonow
float up = 0.0, ui = 0.0, ud = 0.0;
// calka uchybu
static float sum_e = 0.0;
// ostatnia wartosc uchybu
static bool ud_enable = false;
static float last_e = 0.0;
// czlon proporcjonalny
up = Kp * e;
// czlon calkujacy
sum_e += e;
ui = sum_e * h * Kp / Ti;
// czlon rozniczkujacy
if (ud_enable)
ud = (e - last_e) / h * Kp * Td;
ud_enable = true;
last_e = e;
// sterowanie z regulatora
val = up + ui + ud;
// ograniczenie wartosci sterujacej i wylaczenie calki
if (val > max_u) {
val = max_u;
sum_e -= e;
} else if (val < min_u) {
val = min_u;
sum_e -= e;
}
return val;
}
// symulacja ukladu regulacji PID
void closed_loop (float t_sim, float h, float w) {
FILE *f = fopen("closed.txt", "w");
float t = 0.0;
float e, u = 0.0;
state s;
// warunek poczatkowy
s.x1 = 0.0;
s.x2 = 0.0;
while (t <= t_sim) {
fprintf(f, "%.4f;%.4f;%.4f;%.4f;%.4f\n", t, s.x1, s.x2, u, w);
e = w - s.x1;
u = pid (e, h);
s = euler_inert2 (s, u, h);
t += h;
}
fclose (f);
}
int main () {
float h = 0.01; // krok symulacji
float t_sim = 20.0f; // czas symulacji
float u = 1.0; // wartosc sterowania / wartosc zadana
open_loop (t_sim, h, u);
closed_loop (t_sim, h, u);
return 0;
} Plik: pid_script4.m
open = load('open.txt');
closed = load('closed.txt');
figure;
plot (open (:,1), open (:,2), 'b'); hold on;
plot (open (:,1), open (:,3), 'g'); grid on;
title ('Odpowiedz ukladu otwartego');
xlabel ('t [s]');
h = legend ('$y$', '$\dot{y}$');
set(h,'Interpreter','latex')
figure;
subplot (2,1,1);
plot (closed (:,1), closed (:,2), 'b'); hold on;
plot (closed (:,1), closed (:,5), 'r');
plot (closed (:,1), closed (:,3), 'g'); grid on;
title ('Odpowiedz ukladu zamknietego');
xlabel ('t [s]');
h = legend ('$y$', '$w$', '$\dot{y}$');
set(h,'Interpreter','latex');
subplot (2,1,2);
plot (closed (:,1), closed (:,4), 'g'); grid on;
title ('Sterowanie z regulatora PID');
xlabel ('t [s]');
