PID na STM32

Wstęp.

Celem niniejszego projektu, którego charakter jest czysto edukacyjny było zsyntezowanie wiedzy z kilku odrębnych działek. Planem było wykorzystanie systemu mikroprocesorowego do sterowania rzeczywistym układem. Układem miało być coś co jest maksymalnie tanie, proste w budowie i czego model matematyczny nie przyprawia o zawrót głowy. Ostatecznie moje działania doprowadziły do powstania "projektu", który obejmuje elementy wymienione poniżej.

Płytka uruchomieniowa STM32Discovery z $\mu$C STM32F407VGT6 (dokładnie taka: LINK) - wybór tej, a nie innej "platformy" podyktowany był tym, że płytki Discovery są zadziwiająco tanie zważywszy na ich wyposażenie (wbudowany programator, akcelerometr, DAC, mikrofon) oraz uniwersalność samego $\mu$C (168MHz, 1MB flasha, mnóstwo timerów i innych peryferiów w tym kontrolera USB). Nie bez znaczenia jest też duża ilość dostępnej dokumentacji, tutoriali i przykładów wykorzystania procesorów STM32.
Powyższa płytka programowana była z użyciem CooCox CoIDE - moim zdaniem najmniej problematyczne, darmowe i w miarę wygodne środowisko do programowania ARMów.
Mały układzik analogowy zbudowany z dwóch filtrów RC połączonych w szereg - elektronicy zapewne złapią się za głowę ale mi wydało się to całkiem rozsądnym pomysłem aby z kilku rezystorów, diód i potencjometru zrobić "układ dynamiczny".
Aplikacja w środowisku LabVIEW - mała aplikacja do akwizycji i wizualizacji danych z mikrokontrolera. Wybór padł na LabVIEW ponieważ i tak zaistniała potrzeba stworzenia "serial monitora" na potrzeby innego projektu.

Całość działa tak, że z użyciem potencjometru zadawane jest napięcie wejściowe na układ (lub wartość zadana w układzie regulacji), które jest sygnalizowana intensywnością świecenia diody. Następnie mierzone jest napięcie wyjściowe (również sygnalizowane diodą). Choć przydatność tego co zostało zrobione jest dosyć mała to traktuję to jako pierwotną bazę wypadową do czegoś bardziej skomplikowanego. Mam też nadzieję, że może komuś się przyda wiedza/kod tutaj zgromadzone.

Cechy projektu na STM32

Chciałbym w kilku podpunktach opisać cechy programu, który jest rdzeniem całego projektu:

wykorzystanie wbudowanego w STM32 przetwornika ADC wraz z kontrolerem DMA do pomiaru napięć na kondensatorach oraz potencjometrze,
napięcie zadane na wejście układu z użyciem PWM, "wizualizacja" wartości napięcia wejściowego i wyjściowego z użyciem diód z dodatkową linearyzacją ich charakterystyki świecenia,
implementacja cyfrowego regulatora PID wraz z anty-windupem,
implementacja regulatora dwupołożeniowego z histerezą,
symulacja układu ciągłego (inercji II rzędu) z wykorzystaniem RK4,
symulacja układu dyskretnego (podstawienie Tustina),
wykorzystanie kontrolera USB w $\mu$C do transmisji danych do PC; mikrokontroler wysyła z użyciem wirtualnego portu szeregowego stałej długości ramkę ze wszystkimi potrzebnymi parametrami i pomiarami,
wykorzystanie wbudowanego w $\mu$C generatora liczb losowych w celu "symulacji" mocnego zaszumienia.

Dla zainteresowanych udostępniam dwie paczki z projektami CooCoxa. Jedną jest pusty projekt, okrojony do niezbędnego minimum tegoż środowiska (nie potrafię niestety teraz dojść do miejsca skąd udało mi się go pozyskać), który umożliwia komunikację z $\mu$C z użyciem portu USB, zaś drugi to omawiany tutaj projekt.

Korekcja jasności diód została zrealizowana w oparciu o informacje znalezione tutaj: LINK.

Model matematyczny układu RC

Rozpatrywany układ zbudowany jest jak na rysunku:

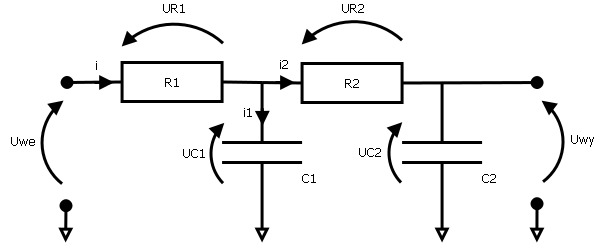
Model matematyczny można wyprowadzić z I i II prawa Kirchoffa otrzymując zgodnie z powyższymi oznaczeniami równania: $$ U_{we} = U_{R_{1}} + U_{C_{1}} \\ U_{C_{1}} = U_{R_{2}} + U_{C_{2}} \\ U_{wy} = U_{C_{2}}, $$ oraz: $$ i=i_1+i_2, \quad U_R=Ri, \quad i_C=C\frac{dU_C}{dt}. $$ Po odpowiednich przekształceniach otrzymuje się ostatecznie liniowe równania różniczkowe: $$ \frac{dU_{C_{1}}}{dt}=-\frac{R_1+R_2}{R_1 R_2 C_1}U_{C_{1}}+\frac{1}{R_2 C_1}U_{C_{2}}+\frac{1}{R_1 C_1}U_{we} \\ \frac{dU_{C_{2}}}{dt}=-\frac{1}{R_2 C_2}U_{C_{2}}+\frac{1}{R_2 C_2}U_{C_{1}}. $$ Za stan układu najwygodniej jest przyjąć napięcia na kondensatorach $\mathbf{x}=\begin{bmatrix}U_{C_{1}} & U_{C_{2}}\end{bmatrix}^T$ zatem macierze układu w przestrzeni stanu dane są następująco: $$ \mathbf{A}= \begin{bmatrix} -\frac{R_1+R_2}{R_1 R_2 C_1} & \frac{1}{R_2 C_1} \\ \frac{1}{R_2 C_2} & -\frac{1}{R_2 C_2} \end{bmatrix}, \quad \mathbf{B}= \begin{bmatrix} \frac{1}{R_1 C_1} \\ 0 \end{bmatrix}, \quad \mathbf{C}= \begin{bmatrix} 0 & 1 \end{bmatrix}, \quad \mathbf{D}=0. $$ Aby otrzymać zapis transmitancyjny można wykorzystać zależność: $$ K(s)=\mathbf{C}(s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B}+\mathbf{D}, $$ lub wykorzystując transformatę Laplace'a oraz kilka przekształceń otrzymując ostatecznie: $$ K(s)=\frac{U_{wy}(s)}{U_{we}(s)}=\frac{1}{R_1 R_2 C_1 C_2 s^2+(R_1 C_2 + R_2 C_2 + R_1 C_1)s+1}. $$ Jak widać, model ten ma jednostkowe wzmocnienie dlatego do ostatecznego układu zdecydowałem się na wejście dodać dzielnik napięciowy zbudowany z dwóch rezystorów. Modyfikuje to nieco układ i wypadałoby model przeliczyć jeszcze raz ale ostatecznie uznałem, że można dzielnik potraktować jako zwykłe wzmocnienie (wzmocnienie mniejsze od jedności).

Aplikacja LabVIEW

Na potrzeby projektu zostało stworzone małe "spaghetti vi", którego zadaniem było odbieranie danych z użyciem portu szeregowego. Dane te były następnie odpowiednio przekształcane i wyświetlane na wykresie. Istnieje też możliwość zapisu danych do pliku. Całość opiera się na pollowaniu portu z użyciem biblioteki VISA. Przykładowe działanie i przebiegi czasowe działającego układu przedstawiono poniżej:

Jeśli ktoś przypadkiem trafi na tę stronę i interesować go będzie którykolwiek z elementów tutaj przedstawionych, proszę o kontakt!