Problem n ciał
Wstęp.
W ramach tego opracowania pochyliłem się nieco nad problemem ruchu n ciał oddziałujących na siebie grawitacyjnie. Problem został przeze mnie tylko nieco liźnięty bo jest to wbrew pozorom bardzo ciekawe i praktyczne zagadnienie, którego złożoność jest znacznie większa niż się początkowo wydaje. Już sam fakt, że po dziś dzień umysły tego świata mają trudności z analitycznym rozwiązaniem tego zagadnienia powoduje, że warto się z tym zapoznać, żeby chociaż wiedzieć z czym to się je. Całość opiera się w zasadzie tylko na prawach fizyki sformułowanych przez Izaaka Newtona. Do tego dochodzi jeszcze szczypta metod numerycznych.
Równania ruchu.
Zgodnie z II zasadą dynamiki Newtona, równanie ruchu ciała o masie skupionej dane jest w postaci: $$ \mb{a}=\frac{\mb{F}}{m}, $$ gdzie: $\mb{a}$ - przyspieszenie, $\mb{F}$ - siła wypadkowa, $m$ - masa ciała. Siła oddziaływania grawitacyjnego dwóch ciał na siebie, zgodnie z prawem grawitacji Newtona przedstawia się następująco: $$ \mb{F}=\gamma\frac{m_1 m_2}{r^2}\mb{\hat{r}}, $$ gdzie: $\gamma$ - stała grawitacji, $m_1$ i $m_2$ - masy ciał, $r$ - odleglość między ciałami, $\mb{\hat{r}}$ - wersor łączący położenia ciał. Jeśli wyznaczana jest siła z jaką ciało 2 działa na ciało 1, to wersor $\hat{r}$ skierowany jest w stronę ciała 2. Korzystając z powyższych zależności można dokonać rozszerzenia problemu na n ciał wyznaczając ich wypadkowe sił oddziaływania oraz równania ruchu: $$ \ddot{\mb{x}}_i=\gamma\sum_{j=1,i\neq j}^{n}m_j\frac{\mb{x}_j-\mb{x}_i}{||\mb{x}_j-\mb{x}_i||^3}, $$ gdzie: $\mb{x}_i$ - trajektoria ruchu ciała i-tego będąca ciągłą funkcją czasu. Aby uzyskać ostatecznie postać poszukiwanych trajektorii należy rozwiązać powyższe równanie różniczkowe dla każdego z ciał. Równanie ruchu ciała dla przypadku dwuwymiarowego można sprowadzić do układu równań różniczkowych: $$ \mb{\dot{x}}=\mb{f}(\mb{x}), $$ gdzie: $\mb{x}=\begin{bmatrix}s_x & s_y & v_x & v_y\end{bmatrix}^T$, $s_x$ i $s_y$ - składowe położenia, $v_x$ i $v_y$ - składowe prędkości. Otrzymuje się ostatecznie postać równań ruchu: $$ \frac{d}{dt}\begin{bmatrix}s_x \\ s_y \\ v_x \\ v_y\end{bmatrix} = \begin{bmatrix}v_x \\ v_y \\ \frac{F_x}{m} \\ \frac{F_y}{m}\end{bmatrix}. $$ Traktując ruch n ciał jako pojedynczy układ dynamiczny należy rozbudować wektor $\mb{x}$ o stan wszystkich obiektów: $$ \mb{x}=\begin{bmatrix}s_{1,x} & s_{1,y} & v_{1,x} & v_{1,y} & s_{2,x} & s_{2,y} & v_{2,x} & v_{2,y} & \dots & s_{n,x} & s_{n,y} & v_{n,x} & v_{n,y}\end{bmatrix}^T, $$ co umożliwia sprowadzanie go do ogólnej postaci równań różniczkowych rozwiązywalnych z użyciem dostępnych metod całkowania numerycznego.
Układ uproszczony. Pierwsza prędkość kosmiczna.
Tematem, który dodatkowo chciałem poruszyć w ramach tego opracowania jest układ uproszczony ruchu dwóch ciał, który idealnie nadaje się do testowania metod całkowania równań różniczkowych. Zakładamy, że jedno z ciał jest znacząco bardziej masywne od drugiego, na tyle, że oddziaływanie tego drugiego jest pomijalne i nie powoduje zmiany położenia ciała cięższego. Układ odniesienia zlokalizowany jest w centrum ciała masywnego. W przybliżeniu można powiedzieć, że przykładem tego typu dwóch ciał jest para Słońce - Ziemia.
Równania stanu satelity, zgodnie z wcześniej przytoczonymi zależnościami dane są w postaci: $$ \frac{d}{dt}\begin{bmatrix}s_x \\ s_y \\ v_x \\ v_y\end{bmatrix} = \begin{bmatrix}v_x \\ v_y \\ -\gamma M \frac{s_x}{(s^2_x + s^2_y)^{\frac{3}{2}}} \\ -\gamma M \frac{s_y}{(s^2_x + s^2_y)^{\frac{3}{2}}}\end{bmatrix}, $$ gdzie: $M$ - masa ciała w centrum. Aby otrzymać stabilną, kołową trajektorię ruchu satelity należy nadać mu odpowiednią prędkość początkową, zwaną pierwszą prędkością kosmiczną. Jej wyznaczenie, przy założeniu braku oporów, możliwe jest poprzez przyrównanie siły dośrodkowej w ruchu po okręgu oraz siły przyciągania grawitacyjnego ciała masywnego: $$ \frac{mv^2}{r}=\gamma \frac{Mm}{r^2}, $$ gdzie: $m$ - masa satelity, $v$ - pozioma (względem powierzchni ciała masywnego) prędkość liniowa satelity, $r$ - promień orbity. Po kilku przekształceniach otrzymuje się ostatecznie zależność wiążącą prędkość satelity oraz jego orbitę: $$ v=\sqrt{\frac{\gamma M}{r}}. $$ Ostatnią rzeczą, której wyznaczenie może się do czegoś przydać jest środek ciężkości układu złożonego z n ciał. Jego współrzędne dane są w postaci: $$ \mb{s}_0=\frac{\sum_{i=1}^{n}{m_i\mb{s}_i}}{\sum_{i=1}^{n}{m_i}}, $$ gdzie: $\mb{s}_0$ - wektor położenia środka ciężkości (barycentrum), $\mb{s}_i$ - wektor położeń ciał.
Implementacja
Na potrzeby tego opracowania stworzono mały skrypt Matlaba, który umożliwia symulacje trajektorii w zasadzie dowolnej ilości ciał. Całkowanie równań odbywa się z użyciem metody RK4. Całą paczkę można ściągnąć tutaj: Download
Paczka zawiera w sobie 3 pliki:
- nBodies.m - skrypt uruchamiający symulację. Aby dodać ciała należy uzupełnić wektor warunków początkowych o 4 kolejne wielkości zgodnie z przyjętą tutaj konwencją. Pamiętać należy również o dodaniu mas następnych ciał do stosownego wektora. Macierz y jest trójwymiarową macierzą o wymiarach: (ilość ciał, 4, ilość kroków symulacji).
- eqOfMot.m - funkcja implementująca równania ruchu n ciał. Pierwszym krokiem jest stworzenie macierzy sił oddziałujących pomiędzy ciałami. Następnie wyznaczane są równania różniczkowe.
- gravForce.m - funkcja obliczająca wartość siły grawitacji pomiędzy dwoma ciałami.
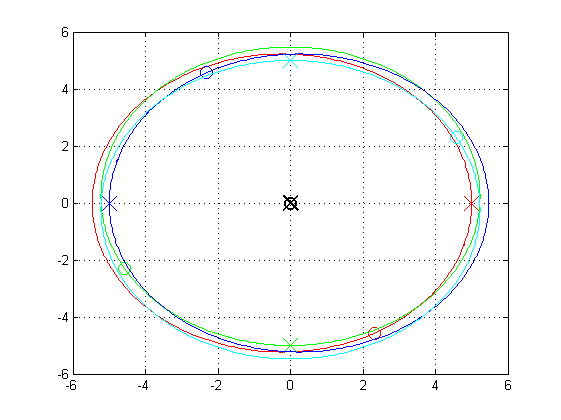
Przykładowe wyniki uzyskane z użyciem wspomnianego kodu przedstawiono poniżej:
 |
 |
 |
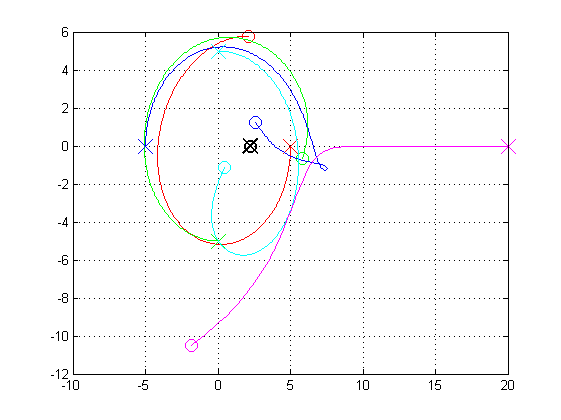 |
Oczywiście lepszy efekt można byłoby uzyskać animując te wykresy, a nie prezentując tylko wyznaczone trajektorie. Będzie to jeden z kolejnych punktów o które będę musiał rozbudować niniejszy "projekt".

