Symulator obiektów dynamicznych
Wstęp
Pomysł ze stworzeniem dedykowanego symulatora obiektów dynamicznych kiełkował w mojej głowie jeszcze za czasu studiów. Było przynajmniej kilka przedmiotów w trakcie których badaliśmy, a potem symulowaliśmy zachowanie konkretnych obiektów dynamicznych. Stąd przyszedł mi do głowy plan napisania "ogólnego" symulatora, który byłby łatwy w konfiguracji, umożliwiał szybkie dodawanie modeli i nie zmuszał do każdorazowego tworzenia układu w Simulinku. Pierwotnie symulator powstał w bardzo okrojonej wersji w Matlabie ale szybko zauważyłem, że obiektowość w Matlabie kuleje, a bez niej ciężko było pewne rzeczy napisać sensownie. Ostatnie wieczory przeznaczyłem więc na wskrzeszenie tej idei i przeniesienie jej do C# (z użyciem WinForms). W ten sposób powstał całkiem sporych rozmiarów projekt, który obejmuje kilka istotnych części. Nabyta niedawno wiedza dotycząca użycia dziedziczenia, interfejsów i innych cudów programowania obiektowego pozwoliła na takie poukładanie kodu, że teraz symulowanie obiektów dynamicznych i klasycznych układów sterowania (mam na myśli układu z regulatorem i ujemną pętlą sprzężenia zwrotnego) jest dość wygodne i przyjemne. Działanie symulatora mocno inspirowane jest działaniem s-funkcji Simulinka.
[Edit 2017-06-25]
Zdecydowałem się na całkowite przepisanie projektu tak, żeby nie straszył i nadawał się do opublikowania. Kod źródłowy dostępny jest tutaj: Control-System-Simulator
Cała solucja podzielona jest na kilka mniejszych projektów, które zostały poniżej opisane nieco szerzej.
JTMath
Projekt zawierający w sobie dwie podstawowe klasy: Vector i Matrix. Pomysł napisania czegoś tak podstawowego jak wektory i macierze zrodził się w momencie kiedy reszta symulatora była już prawie gotowa. Pierwotnie korzystał on z wektorów i macierzy dostępnym w Math.Net. Okazało się jednak, że napisanie własnych implementacji, w bardzo okrojonej wersji, było ciekawym doświadczeniem i idealnym przykładem w którym można użyć testów jednostkowych. Nie wiem jak mogłem żyć do tej pory bez testów. Wymiana obiektów z Math.Net na te napisane przeze mnie przyniosła również znaczący wzrost wydajności symulacji (prawie 3-krotny).
Cechy:
- Vector - implementacja kilku podstawowych funkcji matematycznych wykonywanych na wszystkich elementach wektora, przeciążenie większości potrzebnych operatorów,
- Matrix - implementacja podstawowych funkcji matematycznych, operatorów (np. dodawanie, mnożenie macierzy), wyznacznik i macierz odwrotna (dla macierzy o rozmiarach do 3x3).
Klasa Vector niezbędna jest do działania simulatora w którym wykonują się działania na nich (np. stan obiektu wyższego rzędu jest przechowywane w wektorze). Klasa Matrix wykorzystywana jest w przypadku symulacji obiektu opisanego w przestrzeni stanów.
JTControlSystem
Główny projekt symulatora. Zawiera w sobie wszystkie niezbędne elementy do przeprowadzania symulacji. Zaimplementowano kilka algorytmów całkowania równań różniczkowych (można więcej poczytać o nich tutaj: Całkowanie równań różniczkowych). Symulator umożliwia przeprowadzanie symulacji pojedynczych obiektów lub układów regulacji z ujemnym sprzężeniem zwrotnym (z regulatorem). Możliwe jest przeprowadzenie pojedynczych kroków symulacji jak i wygenerowanie całej serii danych z zadanymi sygnałami wejściowymi. Możliwe jest symulowanie układów ciągłych jak i dyskretnych.
Cechy:
- możliwość symulacji układów ciągłych i dyskretnych, z jednym wyjściem i jednym wejściem (SISO),
- możliwość łatwego dodawania własnych regulatorów (IController),
- możliwość łatwego definiowania własnych obiektów w postaci układu równań różniczkowych/różnicowych oraz równań wyjścia (IContinous i IDiscreteModel),
- możliwość symulacji obiektów zdefiniowanych w postaci funkcji przejścia,
- zawiera obiekt realizujący opóźnienie transportowe,
- zawiera generator sygnałów: prostokątnego, trójkątnego, sinusoidalnego, piłokształtnego,
- zawiera generator sygnału w postaci serii skoków wartości,
- zaimplementowane algorytmy całkowania równań różniczkowych - Eulera, Heuna, MidPoint, Rungego-Kutty, zmodyfikowany algorytm Rungego-Kutty, Dormanda-Prince'a, Adamsa-Bashforta, Adamsa-Moultona,
- umożliwia symulację samego obiektu, obiektu z regulatorem w pętli otwartej, obiektu z regulatorem w pętli zamkniętej oraz układu sterowania, który umożliwia wyłączenie lub włączenie regulatora do toru sterowania,
- obiekt umożliwiający zapis wszystkich danych symulacji do pliku tekstowego.
Dany jest model opisany w przestrzeni stanów: $$ \begin{equation} \mb{\dot{x}}= \begin{bmatrix} 0 & 1 \\ -2 & -3 \end{bmatrix}\mb{x} + \begin{bmatrix} 0 \\ 4 \end{bmatrix}u \\ y = \begin{bmatrix} 1 & 0 \end{bmatrix} \mb{x} + 0u \end{equation}, $$ o niezerowym warunku początkowym oraz regulatora PID o parametrach: $$ K_p=4.2382, \quad T_i=1.5278, \quad T_d=0.1868, $$ Aby przeprowadzić symulację samego modelu oraz zamkniętego układu regulacji można posłużyć się poniższym kodem:
using JTControlSystem;
using JTControlSystem.Controllers;
using JTControlSystem.Models;
using JTControlSystem.SignalGenerators;
using JTControlSystem.Solvers;
using JTControlSystem.Systems;
using JTMath;
namespace ConsoleApp1
{
class Program
{
static void Main(string[] args)
{
// definicja modelu w postaci rownan w przestrzeni stanu
var A = new Matrix(new double[,] { { 0d, 1d }, { -2d, -3d } });
var B = new Vector(new double[] { 0, 4 });
var C = new Vector(new double[] { 1, 0 });
var D = 0d;
IContinousModel model = new StateSpaceModel(A, B, C, D);
// warunek poczatkowy - pamietac o rozmiarach wektorow!
var initialState = new Vector(new double[] { 1d, 0d });
// do rozwiazywania rownan uzyty zostanie algorytm Rungego-Kutty 4 rzedu
ISolver solver = new SolverRK4();
// stworzenie ciaglego systemu na podstawie powyzszego modelu
ISystem system = new ContinousSystem(model, solver, initialState);
// struktura obejmujaca sam system
var bareSystem = new BareSystem(system);
// jako wejscie podana zostanie seria skokow
ISignalGenerator steps = new StepsGenerator(new double[] { 0d, 5d, 10d }, new double[] { 2d, -2d, 2d });
// symulacja
Simulate.Signal(bareSystem, 15d, 0.01d, steps);
// zapis do pliku
FileWriter.ToFile(bareSystem.Data, @"C://bareSystem.txt");
// dodanie regulatora
IController controller = new PID(4.2382d, 1.5278d, 0.1868d);
// zamknieta petla regulacji
var closeLoop = new CloseLoop(system, controller);
// symulacja
Simulate.Signal(closeLoop, 15d, 0.01d, steps);
// zapis do pliku
FileWriter.ToFile(closeLoop.Data, @"C://closeLoop.txt");
}
}
}
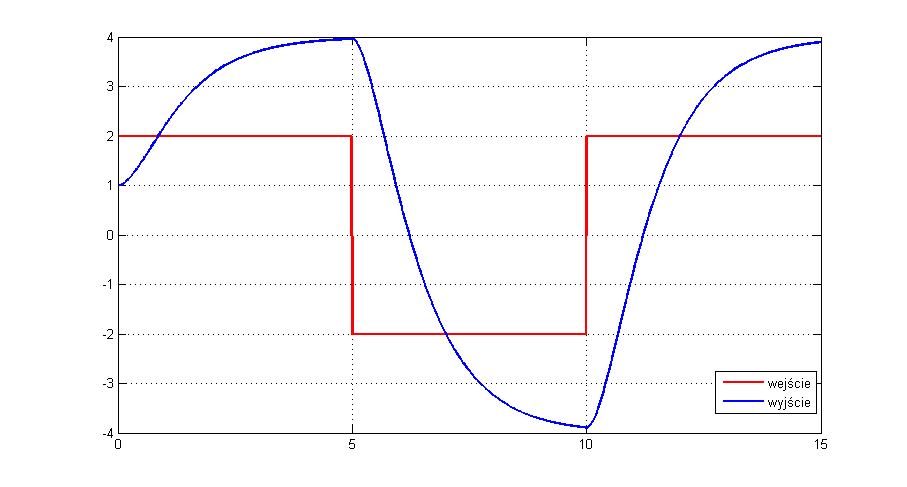
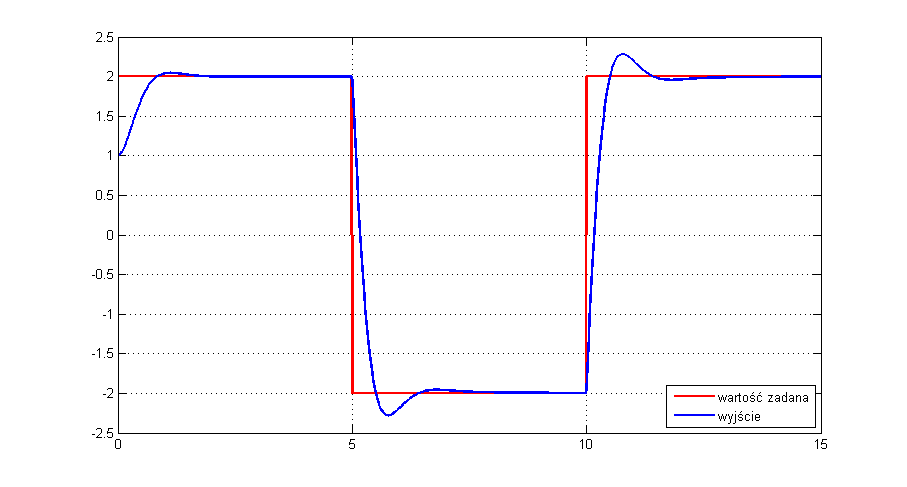
Uzyskane wyniki symulacji przedstawiono poniżej (najpierw sam obiekt, a następnie układ regulacji):
JTControlSystemExamples
Na potrzeby testów stworzyłem przykładowy projekt zawierający sporo przykładów z użyciem JTControlSystem. Projekt zawiera kod uruchamiający zdecydowaną większość funkcjonalności zawartą w głównej bibliotece symulacji.
Uruchomienie przykładów można podejrzeć na filmie:
OfflineSimulator
Pierwotnie funkcjonalność tego symulatora miała zawierać się w symulatorze umożliwiającym symulacje w czasie rzeczywistym. Ostatecznie zdecydowałem się na wydzielenie go jako osobny projekt dla zachowania czytelności.
Cechy:
- możliwość wykorzystania funkcjonalności JTControlSystem,
- możliwość włączenia/wyłączenia sprzężenia zwrotnego (układ otwarty, zamknięty),
- łatwy sposób na definiowanie parametrów i typu sygnału wejściowego,
- graficzne przedstawienie wyników,
- zapis wygenerowanych danych do pliku tekstowego,
- użycie BackgroundWorker do zrównoleglenia dłuższych obliczeń.
Działanie symulatora przedstawiono na poniższym filmie:
RealtimeSimulator
Symulator udostępniający podobną funkcjonalność co wersja offline z tą różnicą, że umożliwia symulacje obiektów w czasie rzeczywistym. Dla uzyskania możliwie największej dokładności licznika wykorzystano bibliotekę MicroTimer (Microsecond and Millisecond C# Timer). Takie posunięcie ma tę zaletę, że licznik zaimplementowany w osobnym wątku może uzyskać dużą dokładność. Do wad należy zaliczyć konieczność pogodzenia wątku licznika z wątkiem GUI (oraz pamiętać o możliwych wyścigach). Większe jest też obciążenie procesora.
Cechy:
- wykorzystanie JTControlSystem do symulacji obiektów ciągłych i dyskretnych,
- użycie dokładnego licznika w celu uzyskania maksymalnej dokładności symulacji,
- odseparowanie kroku symulacji od kroku wizualizacji danych,
- funkcjonalność analogiczna do symulatora offline,
Działanie symulatora przedstawiono na poniższym filmie:
SolversTest
Mały, dodatkowy projekt, który służy do sprawdzania poprawności implementacji algorytmów całkowania równań różniczkowych. Umożliwia on przeprowadzenie testów na zadanym układzie równań równań różniczkowych i porównanie wyniku (liczony jest MSE) z rozwiązaniem dokładnym.
Dla równania różniczkowego w postaci: $$ \frac{dy}{dt}=ty, $$ którego rozwiązaniem analitycznym jest: $$ y(t) = e^{0.5t^2+C}, $$ dla warunku początkowego $y(0)=e$ uzyskuje się rozwiązanie szczególne w postaci: $$ y(t) = e^{0.5t^2+1}. $$ Uruchomienie testu dla takiego układu oraz kilku solverów przedstawia się następująco:
using System;
using JTControlSystem.Solvers;
namespace SolversTest
{
class Program
{
static void Main(string[] args)
{
DifferentialEquations differentialEquation = (state, input, time) => (time * state); // y' = t * y
ExactSolution exactSolution = (time) => (Math.Exp(0.5 * time * time + 1));
Launcher launcher = new Launcher(differentialEquation, exactSolution,
new SolverEuler(),
new SolverEulerTrapezoidal(),
new SolverHeun(),
new SolverMidpoint(),
new SolverRK4(),
new SolverRK4Enhanced(),
new SolverDormandPrince(),
new SolverAdamsBashforth(5),
new SolverAdamsMoulton(5));
launcher.Test(2d, 0.001d);
Console.ReadKey();
}
}
}
zaś uzyskane wyniki: